What Is Structural Analysis in Engineering? Comprehensive Guide

Have you ever wondered about the stability, safety, and efficiency of the cars we drive, the airplanes we travel with, and the house and office where you live and work? And what about that creepy, creaky sound in the skyscraper at night?
Structural analysis is the fundamental and fascinating discipline within engineering that deals with details as structure stability, safety, and efficiency. This article will deal with basic concepts of structural mechanics, methods of analysis, and applications across engineering disciplines, with a particular emphasis on the computer simulation technique known as Finite Element Analysis (FEA) or Finite Element Method (FEM). We'll outline its application in civil engineering structures, automotive projects, and aerospace engineering.
The interplay between disciplines is fascinating. However, we will not delve into solid and fluid interactions since the topic is quite advanced and will be dealt with elsewhere.
We will hint at the role of AI and machine learning as critical facilitators to democratize access to structural analysis software in engineering design departments.
What Is Structural Analysis Engineering?
Structural analysis is the study of structures such as bridges, skyscrapers, cars, or airplanes to predict their behavior under different conditions, such as wind loads impacting a skyscraper, a snow weight on a roof, or a mechanical load on a car component.
Those situations can lead to phenomena such as oscillation and occupant discomfort up to catastrophic failure because of fatigue.
From Mechanical Concepts to Machine Learning - Brief Overview
Structural analysis involves evaluating forces, loads, stresses, and strains on an object or structure to maintain integrity and safety throughout the structure's lifespan. Thus, engineers use this analysis to anticipate weaknesses, assess the impact of external forces, and optimize structures for efficiency and durability.
This is part of an approach called predictive analysis, typically applied in the manufacturing and civil engineering sectors. Such an analysis is based on a solid understanding of physics mathematically translated into partial differential equations. This numerical method couples the geometrical description of the structure (such as with 3D CAD) to produce graphical outputs (3D color maps).
Numerical approximation techniques produce data that can be later fed to machine learning (AI) to reproduce the above CAD-to-output relationship for variable inputs such as geometries or load conditions.
Basic Concepts in Structural Analysis: Loads, Forces, Stress, and Strain
Loads are external forces, forces are internal interactions, stress is force per unit area, and strain is the resulting deformation. For instance, in a beam under load, comprehending forces, stress, and strain ensures structural stability.
Principles of Structural Mechanics: Equilibrium, Compatibility, and Material Behavior
Structural mechanics relies on equilibrium principles to balance forces, compatibility for stability, and understanding material behavior for designing resilient structures.
Equilibrium: Balancing Forces in Structural Mechanics
In structural mechanics, equilibrium transcends a mere balance of forces; it represents a harmony between internal and external forces acting on a structure. The equilibrium principles dictate that the sum of forces and moments within a structure must be zero to ensure that the structure remains static and does not undergo undesired deformations or movements.
Achieving equilibrium involves meticulous consideration of external loads, reactions at supports, and internal forces within structural elements. Engineers meticulously apply equilibrium equations, such as those derived from Newton's laws, to ensure the balancing of forces, contributing to structure stability and resilience.
Compatibility: Orchestrating Deformations for Structural Stability
The notion of compatibility embodies the orchestration of deformations within a structure to maintain stability and prevent structural failure, such as a bridge failing under wind loads. In essence, compatibility ensures that the interconnected structure components respond harmoniously to external loads and internal forces. This involves a nuanced understanding of how deformations propagate through different structural elements, requiring engineers to address issues such as material elongation, contraction, and rotation.
By ensuring compatibility, engineers guarantee that a structure remains internally consistent, preventing unintended distortions and guaranteeing stability under varying conditions.

Material Behavior: Crafting Resilient Structures through Insightful Design
Understanding material behavior is not merely a prerequisite but an art form within structural mechanics. Beyond acknowledging basic properties like elasticity and strength, it involves delving into the intricate responses of materials to different loading conditions.
Engineers must compute how materials undergo stress, strain, and deformation under various forces, temperature variations, and environmental factors. The triad of equilibrium, compatibility, and material behavior forms the cornerstone of structural mechanics. It's not a rigid framework but a dynamic interplay that any structural engineer manipulates to create structures that endure and respond to changing conditions in engineering design.
Methods of Structural Analysis: Analytical Methods
Analytical methods use equations to determine internal forces and deformations. Distinguishing between determinate and indeterminate structures, statics, and dynamics is crucial.
Determinate and Indeterminate Structures
Structures are categorized as either determinate or indeterminate based on the number of unknown forces and reactions that can be determined using equilibrium equations.
Determinate structural elements have a sufficient number of equations to solve for all unknowns, while indeterminate structures involve more unknowns than available equations. Analyzing indeterminate structures often requires additional compatibility equations or methods, such as the flexibility or stiffness matrix approach.
Statics of Structures
Statics is a branch of mechanics that deals with structures in a state of equilibrium, i.e., structures at rest. It involves the study of forces, moments, and reactions acting on stationary structures. By applying the principles of equilibrium, static analysis allows engineers to calculate forces and displacements in different elements, ensuring that the structure remains stable under various applied loads.
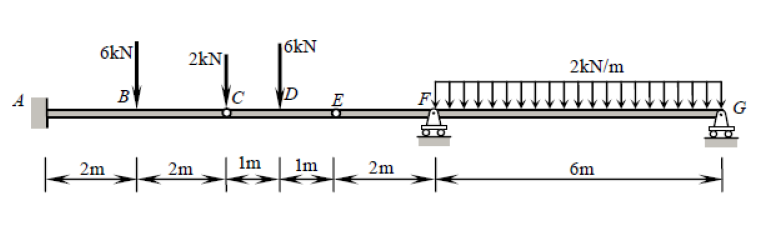
Dynamics of Structures
Dynamics focuses on structures in motion - for instance in the response of structures subjected to dynamic loads such as earthquakes, wind, or machinery vibrations. Dynamics involves studying the time-dependent behavior of structures and may require advanced techniques like modal analysis or time-history analysis.
Numerical Methods - Focus on the Finite Element Analysis Process
Numerical methods, particularly the Finite Element Method (FEM) numerical solution method, are indispensable for complex structural analyses.
FEM is a numerical method that mathematically divides structures into simple structures called finite elements, enabling detailed simulations. Its application extends to solving problems in various engineering fields.
Simulations are possible because numerical methods such as a matrix finite element analysis are implemented, and in turn, numerical methods imply solving differential equations generated from the underlying physics and mechanics of the structures being analyzed.
Finite Element Method (FEM) in Detail
The Finite Element Method is a numerical technique used to analyze structural behavior under different conditions. It breaks down complex structures into smaller, more manageable elements.
At its core, FEM operates on the principle of discretization, transforming a continuous and intricate structure into a finite number of simpler elements. These very simple structural elements, often geometrically shaped, such as triangles or quadrilaterals in two dimensions or tetrahedra and hexahedra in three dimensions, collectively represent the entire structure.
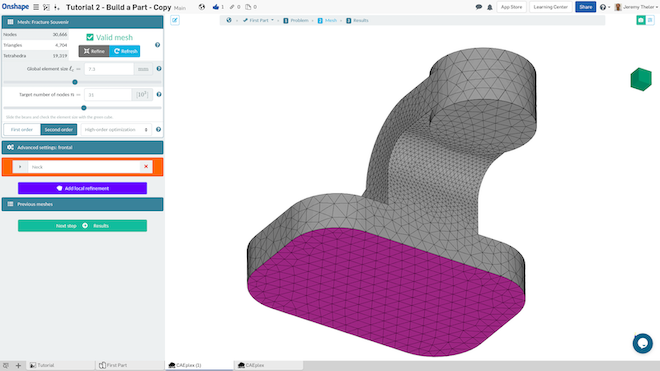
Discretization Process in the Finite Element Approach
The first step in applying FEM involves breaking down the structure into finite elements; thus the finite element method approximates a continuum behavior. This is akin to dividing a puzzle into smaller, more manageable simple structures. Each element serves as a representative unit, and collectively, they form a mesh that covers the entire structure. The choice of element type and size is a critical consideration, as it impacts the accuracy and efficiency of the analysis.
Once the structure is discretized, structural analysis software analyzes each element. Within these elements, engineers apply mathematical models that simulate the physical behavior of materials under various conditions. These models consider factors such as material properties, external structural loads, and boundary conditions. Mathematical equations derived from the principles of equilibrium, compatibility, and material behavior (see above) are then solved to determine the element's response.
A hallmark of FEM is its ability to capture the interactions between neighboring elements. Each element affects and is affected by its adjacent counterparts, creating a cohesive structure representation. This interconnectedness is vital for accurately predicting how forces and deformations propagate throughout the structure.
Assembly and Solution
As the analyses of individual elements unfold, the next step involves assembling the results into a comprehensive system of equations. This system encapsulates the entire structure and embodies the relationships between elements. Advanced numerical methods, such the matrix method, are then employed to solve these equations, yielding the complete response of the structure.
Validation and Iterative Process
The accuracy of FEM hinges on the iterative nature of its process. Engineers validate the results by comparing them to theoretical expectations or experimental data. Discrepancies may lead to adjustments in the discretization, element types, or boundary conditions, refining the analysis until it converges to a solution that accurately reflects the real-world structural behavior.
Applied Finite Element Analysis in Civil Engineering
In civil engineering, Finite Element Analysis has become a cornerstone in structural analysis. For example, in the design of a suspension bridge, FEM allows engineers to model and analyze the intricate forces acting on different components. This simulation provides insights into how the bridge will respond to various loads, ensuring its safety and efficiency.
Moreover, FEM is extensively applied in the analysis of high-rise buildings. Engineers can simulate real-world conditions such as wind loads, seismic activities, and occupancy factors to optimize the building's design. This ensures that the structure not only meets safety standards but also performs efficiently throughout its lifespan.
The versatility of FEM extends to other civil engineering projects, including dams, tunnels, and stadiums. Its ability to handle complex geometries and varied material properties makes it an invaluable tool for engineers seeking precision in their structural analyses.
Applications of Structural Analysis
We will present a few examples of structural analysis applications in different industries, starting from the civil engineering sector.
Civil Engineering Structures Examples
Consider a large-scale civil engineering project, such as the construction of a dam. FEM can be employed to model the complex interactions between the dam structure, the water it retains, and the surrounding soil. This simulation helps engineers assess the dam's stability under different water levels, ensuring its safety and reliability.
Another application is in tunnel construction. FEM aids in analyzing the stress distribution along the tunnel walls, considering factors like soil pressure and the weight of the overlying rock. This ensures the tunnel remains structurally sound and can withstand varying geological conditions.
FEM is not limited to the design phase. It is also extensively used in monitoring structures during their lifespan. For instance, in a bridge, FEM can be employed to assess how the structure's integrity may change over time due to factors like corrosion, wear and tear, or unexpected events. This proactive approach allows engineers to implement maintenance and repair strategies before issues escalate.
Mechanical Engineering Applications From Various Industries
In mechanical engineering, structural analysis is crucial for designing machinery, aerospace structures, and automotive components. It ensures structural integrity for optimal performance and safety.
Precision in Machinery Design
In machinery design, structural analysis is a meticulous process used to examine the forces, loads, and stresses that components endure during operation. Through rigorous analysis, engineers refine designs to eliminate weak points, reduce vibrations, and enhance load-bearing capacities. This precision ensures the longevity of machinery and directly influences its efficiency, contributing to seamless operations in various industries.
Aerospace Structures: Meeting Demanding Conditions
In aerospace engineering, advanced structural analysis is instrumental in addressing the challenges posed by gravitational forces, atmospheric pressures, and dynamic flight conditions. It is essential for ensuring airworthiness. Engineers focus on understanding how materials withstand extreme temperatures, aerodynamic forces, and the stresses of flight. The application of structural analysis in aerospace design guarantees that every component can withstand the rigors of flight, ensuring safety and mission success.

Automotive Components: Balancing Safety and Performance
In the automotive industry, structural analysis typically is used for assessing the impact of collisions, vibrations, and varied road conditions on vehicle structures. A normal notebook cannot be considered as sufficient computing power and HPC clusters or cloud computing is needed.
Beyond the chassis, it extends to every component, from the suspension system to the frame. Structural analysis influences the design of safety features, optimizing material selection, and ensuring that vehicles perform well and protect occupants in accidents while respecting economic and environmental constraints.
Beyond Traditional Boundaries: Emerging Trends
As mechanical engineering evolves, structural analysis facilitates innovative solutions and emerging trends. The integration of smart materials, coupled with advancements in analytical and computational development tools, enables real-time monitoring of structural health in machinery and vehicles. Predictive maintenance strategies, informed by structural analysis, redefine how mechanical systems are managed, minimizing downtime and optimizing performance.
Structural Analysis Software and Tools - Finite Element Analysis
Comparing and contrasting different tools is crucial. Understanding the strengths, limitations, and applications of structural analysis tools helps engineers choose the most suitable ones.
Comparative Analysis of Finite Element Analysis Software
Several structural analysis software tools are widely used by modern structural engineers. A comparative analysis can shed light on their features, strengths, and limitations. While not in the position to issue any judgment, we will shed light on some widely known names such as ANSYS or NASTRAN. By evaluating these tools, engineers can make informed decisions based on their specific project requirements.
ANSYS is recognized for its versatility and capabilities in finite element analysis (FEA). It is a comprehensive software suite that covers structural, thermal, and fluid dynamics analyses. ANSYS can handle complex simulations involving a variety of physical phenomena. Its wide range of tools makes it suitable for diverse engineering applications, from automotive to manufacturing.
Originally developed by NASA in the '60s and later commercialized by the MacNeal-Schwendler Corporation (MSC), NASTRAN (NASA Structural Analysis) has become an aerospace industry standard for finite element analysis. It's renowned for its accuracy and reliability, as well as in automotive engineering. NASTRAN provides a robust platform for linear and nonlinear structural analysis, offering precise solutions for complex structural problems.
The Moment Distribution Method
The Moment Distribution Method is a separate structural analysis technique often applied to statically indeterminate structures, especially continuous beams and frames.
The method was developed to simplify the analysis of such structures by distributing moments throughout the structure until equilibrium is achieved.
Here are the key steps involved:
1. Indeterminate Structures: The method is applied to structures with more unknowns (degrees of freedom) than available equilibrium equations. Examples include continuous beams with overhangs, frames with hinges, and other statically indeterminate structures.
2. Distribution of Fixed-End Moments: Begin by applying fixed-end moments at fixed or restrained support locations in the structure. These initial moments are usually assumed and used to create a statically determinate system.
3. Distribution of Moments: The total fixed-end moments at each support are distributed to adjacent members based on their relative stiffness. The distribution of moments is carried out iteratively until equilibrium is reached. The relative stiffness of each member influences the amount of moment transferred at the supports.
4. Carryover of Moments: During each iteration, a portion of the moments is "carried over" to the adjacent member. The carried-over moments are added to the initial moments at each support, and the process is repeated until the moments converge to a consistent set of values.
5. Convergence: The iteration process continues until the moments at each support no longer change significantly between iterations. This is the point of convergence, indicating that the distribution of moments has reached equilibrium and the structure is stable.
6. Calculation of Reactions and Member End Moments: Once the system has reached equilibrium, reactions at supports and moments at member ends can be calculated using the distributed moments. These values can then be used to determine member forces and displacements.
Advantages: It simplifies analysis and can be used in uncertain situations. It provides external forces.
Limitations: It requires assumptions about member stiffness and joint placement. Advanced methods, like the Finite Element Method, are often more efficient and precise.
The Role of a Structural Engineer
Structural engineers play a central position in the construction and mechanical industry, contributing significantly to the inception, development, and completion of a wide array of structures. Their responsibilities encompass various tasks, ensuring the integrity, safety, and efficiency of the built environment.
At the forefront of their duties is the evaluation of construction processes. Structural engineers scrutinize every phase of the construction journey, from the laying of foundations to the installation of structural components. Through analysis and oversight, they check that each step aligns with industry best practices, regulatory requirements, and design specifications. This evaluation serves to mitigate potential risks and ensures that construction proceeds in a manner that upholds structural integrity.
Compliance with high-quality standards is key. These professionals are charged with the responsibility of verifying that all materials used in construction meet stringent quality benchmarks. By conducting inspections and assessments, they guarantee that the structural elements, be it concrete, steel, or other materials, possess the durability and resilience necessary to withstand the demands imposed by environmental factors and loads.
The assessment of materials and equipment extends beyond quality checks, encompassing considerations of appropriateness for the specific project. Structural engineers are tasked with selecting materials that meet the project's design requirements and align with economic constraints and sustainability objectives. This involves understanding material properties, construction methods, and the environmental impact of each choice.
Integral to the structural engineer's role is the design of comprehensive construction plans. These plans serve as the blueprint for the entire construction process, detailing the arrangement and specifications of structural elements. The engineer employs advanced computational tools, such as finite element analysis, to predict and optimize structural performance under varying conditions. This forward-looking approach ensures that structures meet safety standards upon completion and maintain their reliability throughout their entire lifecycle.
Challenges and Future Trends in Structural Analysis
As technology evolves, new challenges and trends emerge in structural analysis. Advancements in materials, computational power, and artificial intelligence are shaping the future of this discipline.
Challenges
Scale and Complexity: With the design of larger and more complex structures, structural analysis faces the challenge of handling vast amounts of data and intricate geometries.
Interdisciplinary Integration: As projects become more interdisciplinary, structural analysis must seamlessly integrate with other engineering disciplines like environmental and geotechnical engineering.
Sustainability: The increasing emphasis on sustainable design requires structural analysis to consider environmental impacts, life cycle assessments, and energy-efficient structures.
Future Trends
Advanced Materials: Using innovative materials, such as carbon-fiber composites and self-healing materials, will influence structural analysis methods and considerations.
Digital Twins: The concept of digital twins, creating a virtual replica of a physical structure, offers opportunities for real-time monitoring, predictive maintenance, and improved decision-making throughout a structure's life.
AI and Machine Learning: Integrating artificial intelligence and machine learning into structural analysis tools can enhance predictive capabilities, optimize designs, and improve efficiency.
Conclusion
Structural analysis is a true cornerstone of engineering, ensuring the safety and efficiency of structures. Because of its infinite range of applications in civil engineering and other sectors such as automotive or aerospace, the Finite Element Method is a powerful tool for detailed simulations and optimization. The examples illustrated its practical application in various projects and future trends with Machine Learning (AI).



