What Is Geometric Modeling? Types & Applications

Representing physical objects in digital form is a given in contemporary industries. Apart from raw sketches for preliminary concept design, any engineer now thinks of objects designed in 2D or 3D digital spaces.

This article explores the fundamental concepts, types, and applications of geometric modeling: geometric modeling of shapes is a crucial aspect of design and visualization, and knowledge of how they are represented helps not only the geometric shapes representation with Computer Aided Design (CAD) innovations but also advanced approaches such as simulation with finite element analysis and optimization algorithms to achieve the desired shape.

Understanding the Basics

Geometric modeling relies on foundational principles, including elementary mathematical concepts and geometric transformations. Readers will appreciate the precision and versatility of theoretical mathematical geometric modeling and its application to computer geometric modeling.

Looking forward to advanced applications, those concepts are indispensable to building basic digital shapes for constructing the framework structure for finite element and fluid dynamic simulation, i.e., computational meshes. Starting from spatial boundaries of objects, 3D simulation software can achieve predictions where analytic functions are not available because of the problem complexity. Starting from wire frame models or solid modeling in CAD programs, simulation programs define polygonal surfaces that represent the "surface mesh" and operate on the filled volume of the shape with various elements (in the case of fluid dynamics, called finite volumes) that are used for lengthy numerical computations. The AI task is to shorten those lengthy numerical computations into real-time predictions.

Back to the basics now! This section explores the elementary concepts forming the backbone of geometric modeling, emphasizing their role in creating and representing virtual objects.

Elementary Mathematical Concepts in Geometric Modeling

Geometric modeling relies on fundamental principles in mathematics and geometric transformations. Central to geometric modeling is a mathematical concept set as a framework for defining and describing digital objects, including points, vectors, curves, and surfaces.

As a fundamental element of modeling, points, in mathematical terms, represent a location in space. In the digital realm, points are building blocks for constructing more complex geometric entities.

Vectors, directional quantities with both magnitude and direction, represent translations and orientations in geometric modeling.

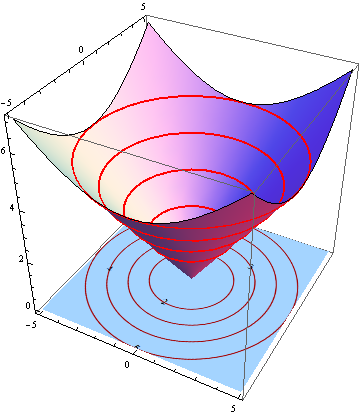
Curves are mathematical entities that define the path of a point in space. Represented parametrically, a 2D curve has the following mathematical description:

r(t) = < x(t), y(t), z(t) >

where "t" is a parameter over a specified interval, parametrizing the curve. Curve types can include Bézier curves and B-splines, expressed as weighted combinations of control points.

Finally, surfaces are mathematical constructs that define the boundaries of 3D shapes represented with the following mathematical description of a parametric surface:

r(u,v) = (x(u,v), y(u,v), z(u,v))

where two variables, "u" and "v" parameterize surfaces.

Examples of a surface model include parametric surfaces, defined through functions, and Bézier surfaces, expressed as combinations of control points. These mathematical models facilitate precise control over the shape and characteristics of surfaces in geometric modeling.

Geometric Transformations: Manipulating Digital Entities

Geometric transformations form the backbone of geometric modeling, enabling the dynamic manipulation of digital entities with precision and versatility.

Three fundamental transformations—translation, rotation, and scaling—are pivotal in shaping virtual geometric objects.

Translation shifts geometric entities along a specified direction in space. By applying translation, digital objects can be moved to new positions without altering their shape or orientation.

Rotational transformations revolve around changing the orientation of geometric entities. Engineers and designers use rotations to position objects at specific angles, allowing for exploring design variations.

Scaling transformations alter the size of objects, either enlarging or reducing them proportionally. This operation is instrumental in adjusting dimensions and proportions within the digital space.

Types of Geometric Modeling: A Breakdown

Distinguishing between 2D and 3D modeling is basic to understanding geometric modeling. This section provides a technical overview starting from the underlying mathematical principles.Wireframe Geometric Modeling and Applications

Wireframe modeling, integral to Computer-Aided Design (CAD) as used in CAD programs, is a fundamental technique for engineers and designers. This exploration delves into wireframe geometric modeling, dissecting its characteristics, applications, and limitations.

Wireframe modeling is a foundational geometric modeling approach in CAD software, representing a three-dimensional geometric model through a network of lines and curves. These elements, known as edges, outline the structure of the object's geometry without delving into surface details. It is a "minimalist" representation, focusing solely on the essential framework. This makes wireframe geometric modeling an efficient method for conceptualizing and visualizing complex structures.

Each line or curve holds critical geometric information in wireframe geometric modeling, specifying the connectivity between points and defining the object's edges. This simplicity facilitates rapid model creation and modification, a crucial aspect of the iterative design process.

Wireframe modeling finds extensive applications in product design, providing engineers with a versatile tool to conceptualize and refine their ideas. The simplicity of wireframes allows for quick ideation and exploration of design variations. This is particularly beneficial in the early stages of product development when multiple concepts are being considered.

Engineers use wireframe geometric modeling to define a product's basic geometric object and structure before moving on to more detailed representations. It serves as a visual guide, aiding in evaluating proportions, spatial relationships, and overall aesthetics. Additionally, the lightweight nature of wireframe models makes them computationally efficient, contributing to smoother collaboration and faster design iterations.

One key strength of wireframe modeling is its utility for representing object structures. By focusing on the underlying framework, wireframes convey the spatial arrangement of components within a design.

For complex machinery, architectural structures, or intricate mechanical components, wireframe geometric modeling provides a clear visualization of how different parts interact and fit together.

While wireframe modeling offers efficiency and simplicity, it comes with inherent limitations. One primary drawback is the lack of surface information. Wireframe models cannot convey realistic visualizations of the final product without explicit surface representation. This limitation makes them less suitable for presentations or client-facing visuals where a high level of realism is required.

Another consideration is that wireframe geometric modeling may not accurately capture complex geometries or intricate surface details. Other surface or solid modeling might be more appropriate when surface finish, texture, or intricate curves are crucial to the design.

Surface Modeling: Mathematical Representation and Challenges

The creation of surfaces and their mathematical representation is a technique explored in this section. A discussion of inherent challenges in surface modeling techniques accompanies applications in product design and animation. A technical perspective on the intricacies of surface modeling provides readers with a deeper understanding of its role in achieving realistic digital representations.

Surface modeling is rooted in mathematical representations that define the geometry of an object's external features. Unlike wireframe models, surface models go beyond structural frameworks and aim to capture the complex surfaces that define a product's visual and tactile characteristics.

Mathematically, surfaces can be described using various methods, such as parametric equations, spline curves, and NURBS (Non-Uniform Rational B-splines). Parametric equations define the coordinates of points on the surface in terms of parameters, offering precise control over shape and continuity. Spline curves, including Bézier and B-spline curves, are widely used for smooth and flexible surface representations. NURBS, a mathematical representation using rational functions, excels in representing complex and free-form surfaces.

What are the applications for surface modeling?

Surface modeling finds extensive application in product design, where achieving realistic and aesthetically pleasing surfaces is paramount. Engineers and industrial designers use it to produce a final geometric model for consumer products, automotive components, or electronic devices. Representing smooth curves and intricate details is crucial for designing functional and visually appealing products.

In computer graphics animation, surface modeling is instrumental in creating lifelike characters and environments. By defining the surfaces of 3D models, computer graphics animators can bring virtual worlds to life with realism. Surface models are used to simulate the behavior of light on different materials, allowing for the creation of visually convincing animations.

Designing complex machinery, like those used in the automotive and aerospace industries, involves precision, maintenance, accessibility, and safety challenges. Intricate mathematical calculations and virtual 3D modeling are added to the complexity to ensure precision and accuracy.

Geometric solid modeling allows engineers, architects, and designers to create realistic virtual representations of physical objects as geometric solid models. This technique transforms ideas into representing solid models in 3D, with a final solid shape in the virtual space.

It's a mathematical approach to representing objects in a digital space that introduces the concept of volume, creating shapes with depth, breadth, and height. The fundamental building blocks of this technique are mathematical primitives such as spheres, cubes, cones, and cylinders, which, when assembled, form complex and realistic structures.

Geometric solid modeling is parametric.

Parametric modeling involves defining the object's dimensions and characteristics using parameters. This introduces a level of flexibility that is invaluable in the design process. Engineers and designers can easily modify parameters to alter the model's geometric shapes, sizes, or attributes without starting from scratch.

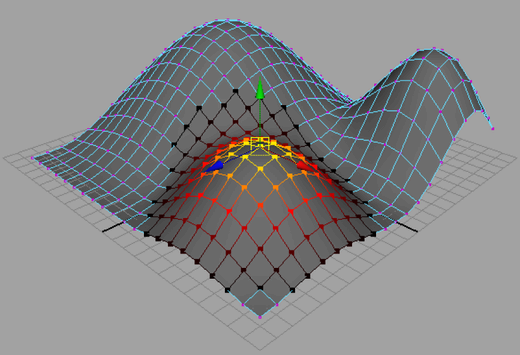
Constructive Solid Geometry: Building Complexity from Simplicity

Constructive solid geometry is a vital technique within geometric solid modeling. Constructive solid geometry combines simple geometric primitives through Boolean operations like union, intersection, and subtraction to create more complex geometric shapes.

Constructive solid geometry provides an efficient and intuitive way to generate complex structures with precision.

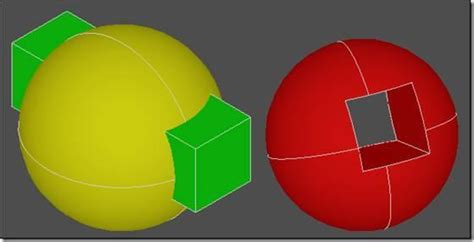
(B-Rep): Capturing Surface Details

In geometric solid modeling, the boundary representation ("B-Rep") method captures the details of an object's surfaces. B-Rep represents the solid by specifying its boundaries, including faces, edges, and vertices. This methodology is particularly advantageous in conveying surface characteristics crucial for visualization and analysis. It enables the creation of solid models with accurate volumes and realistic surface qualities.

Applications Across Industries

Geometric solid modeling finds extensive applications across diverse industries, profoundly impacting fields such as engineering, manufacturing, architecture, and computer geometric modeling (CAD).

In engineering, geometric solid modeling is the cornerstone of product design. Engineers use this technique to create detailed representations of mechanical components, ensuring precision in dimensions and functionality. Whether designing automotive parts, machinery components, or intricate devices, geometric solid modeling provides the accuracy required for prototyping and manufacturing.

Geometric solid models also serve as the blueprint for manufacturing processes. By translating digital models into physical objects through techniques like computer numerical control (CNC) machining or 3D printing, manufacturers can replicate the exact specifications outlined in the geometric solid model. This seamless translation from the digital to the physical realm enhances efficiency and accuracy in production.

Challenges and Future Developments

While geometric solid modeling has revolutionized how we design and manufacture objects, it's not without challenges. Managing complex models with numerous parameters can be computationally demanding, requiring powerful hardware for efficient processing.

Advancements in geometric solid modeling are expected to address these challenges. Integrating artificial intelligence and machine learning may enhance the automation of design processes, allowing systems to generate and optimize geometric models intelligently. Furthermore, developments in real-time rendering technologies will contribute to more immersive and interactive design experiences.

Technical Advancements in Visualization

Architects leverage geometric modeling for visualizing buildings and structures, and this article delves into the technical applications within Building Information Modeling (BIM) systems. Technical insights into how geometric modeling enhances project management and communication in the architecture and construction sectors are examined.

At the core of architectural and civil engineering projects lies the need for design and visualization. Geometric modeling provides architects and engineers with a toolset to bring their concepts to life in a virtual environment. From conceptualizing structures to refining details, architects leverage 3D geometric models to visualize and refine their designs. This enhances the creative process and allows stakeholders to understand the proposed structures better before they materialize.

One of the most transformative applications of geometric modeling in architecture and civil engineering is Building Information Modeling (BIM), which creates and manages digital representations of a building or infrastructure's physical and functional characteristics. Geometric modeling forms the backbone of BIM, enabling the creation of intelligent 3D models that store not just visual data but also crucial information about materials, costs, and timelines.

Structural Analysis and Simulation

Geometric modeling is a cornerstone in conducting structural analysis and simulation in civil engineering. Engineers utilize 3D models to simulate how structures respond to various conditions such as loads, environmental factors, and seismic events. The ability to run these simulations on geometric models ensures that the final structures meet safety standards and performance expectations.

Geometric models serve as the foundation for Finite Element analysis simulations. They are imported into FEA software and divided into finite elements for analysis. Material properties and boundary conditions are used to replicate real-world scenarios accurately. Engineers use software to conduct simulations and assess structural performance. Insights from FEA simulations are used to iteratively refine the geometric model iteratively, enhancing the overall design process.

Urban Planning and Spatial Analysis - Conclusion

In the realm of urban planning, geometric modeling aids in creating detailed representations of entire cityscapes. This includes the modeling of buildings, roads, utilities, and green spaces. With these comprehensive 3D models, urban planners can analyze the spatial relationships between different geometric elements, optimize traffic flow, and make informed decisions about the allocation of resources. Geometric modeling, therefore, becomes a crucial tool in creating sustainable and efficient urban environments.

Effective communication is key in architecture and civil engineering projects, especially with diverse stakeholders. Geometric modeling provides a common visual language that bridges the gap between technical experts, clients, and the general public.

In conclusion, the applications of geometric modeling in architecture and civil engineering are vast and transformative. From initial design concepts to the construction phase and beyond, this technology significantly enhances efficiency, accuracy, and communication, making it an indispensable tool in the modern built environment. As technology advances, the integration of geometric modeling will likely further shape the future of architectural and civil engineering practices.

What's Next? AI Revolution in Engineering!

The next step is a new implementation of Artificial Intelligence related to engineering predictive capabilities.

How is this related to geometric modeling?

The most recent Deep Learning, Computer Vision-based advances are indeed applied to real-time interpretation of CAD software in terms of engineering performance indices.

In practice, while not being a "general AI, " Deep Learning with specific neural networks can predict physical properties associated with object shapes.

All this happens within a very reduced computer time.

In the end, CAD system users can access advanced predictive capabilities without toils and model quicker and better desired industrial shapes. In terms of business, this helps achieve scaling of the simulation solutions from a small circle of experts to the whole demographics of engineers within a corporation.