Vibration Testing Basics: Methods and Applications

Experimental vibration testing is a diagnostic tool for identifying, monitoring, and mitigating potential failures within machinery, such as rotating and reciprocating machines. Thus, engineers can preemptively address issues before they escalate into costly downtime or even catastrophic failures.

While, as CAE or Deep Learning engineers, we are concerned with simulations, our vibration testing colleagues work in the lab or on the field collecting data from vibration sensors and capturing critical parameters such as amplitude, frequency, and phase.

We will review the adverse effects of vibration on machines and buildings, thus explaining the importance of vibration tests even, not only for on-the-field operation but also to influence preemptive engineering design in the early concept phases.

Why Vibration is Important

Vibration-induced mechanical failure occurs when dynamic forces exceed the structural integrity of a component or system, leading to degradation or catastrophic failure. This phenomenon can be explained with structural dynamics and material science, incorporating mathematical formulations to illustrate the underlying mechanisms.

Vibration-induced mechanical failure is influenced by fatigue, resonance, and wear factors. With experimental vibration testing and CAE simulation, engineers can predict and mitigate the effects of vibration, thereby enhancing the reliability and longevity of mechanical systems. The discipline of AI Deep Learning, feeding on the data generated by tests and simulation from vibration testing labs, can aid with new insights based on its speed or response and capability to explore a wide design space within an unprecedentedly reduced time, and it can be deployed at a very early stage of the design process.

Vibration-induced fatigue failure occurs when cyclic loading leads to progressive damage accumulation in a material, ultimately resulting in fracture. The S-N curve, depicting the relationship between stress amplitude (σ) and number of cycles to failure (N), is commonly utilized to characterize fatigue behavior. Mathematically, the S-N curve can be expressed as:

N = (σ_max / σ_f)^(-1/m)

where N is the number of cycles to failure, σ_max is the maximum stress amplitude, σ_f is the fatigue strength coefficient, and m is the fatigue exponent.

Excessive vibration can cause stress concentrations and microstructural changes, accelerating fatigue crack initiation and propagation, ultimately leading to failure.

Resonance occurs when the natural frequency of a system coincides with an external excitation frequency, resulting in amplified vibrations. The dynamic response of a single-degree-of-freedom (SDOF) system subjected to harmonic excitation can be described by the equation:

m d²x/dt² + c dx/dt + k x = F_0 cos(ωt)

Resonance-induced vibrations can lead to excessive stress and displacement amplitudes, causing fatigue failure or structural damage.

Vibration can induce fretting wear and looseness in mechanical assemblies, leading to accelerated degradation and potential failure. The wear rate (W) due to fretting can be quantified using Archard's equation: W = k F s where k is the wear coefficient, F is the normal force, and s is the sliding distance. Vibration-induced fretting wear can result in increased clearances, loss of preload, and eventual failure of fasteners or bearings.

Three Pillars for Vibration Investigations: Vibration Testing, CAE Simulation and AI

Experimental Testing, CAE Simulation, and Artificial Intelligence (AI) are three distinct approaches employed by vibration engineers to analyze and mitigate vibration-related issues in machinery.

Experimental Testing

Experimental testing involves the physical measurement and analysis of vibrations in real-world scenarios. Vibration engineers use sensors and data acquisition systems to collect data directly from machinery during operation or controlled tests in laboratory settings. This approach provides accurate and reliable data on vibration levels, frequencies, and other parameters, allowing engineers to diagnose existing problems, validate theoretical models, and assess the effectiveness of mitigation strategies. Experimental testing offers a comprehensive understanding of machinery behavior under operating conditions, making it a valuable tool for vibration analysis and diagnostics.

CAE Simulation and Vibration Analysis

Computer-aided engineering (CAE) simulation involves using computational models and numerical methods to simulate and analyze the behavior of machinery under various vibration conditions. Vibration engineers develop mathematical models of mechanical systems, incorporating factors such as material properties, geometry, boundary conditions, and external loads. These models are then solved using numerical techniques, such as finite element analysis (FEA), to predict vibration responses, stress distributions, and other relevant parameters. CAE simulation allows engineers to explore different design alternatives, optimize structural configurations, and evaluate the impact of vibration on system performance without the need for physical prototypes. It enables cost-effective and efficient analysis of complex vibration phenomena, facilitating the design and development of robust and reliable mechanical systems.

Artificial Intelligence (AI) and Vibration Analysis

Artificial Intelligence (AI) can be applied to use machine learning techniques to analyze, interpret, and act upon vibration data autonomously. Vibration engineers can employ AI algorithms to process large volumes of sensor data, identify patterns, anomalies, and trends, and make decisions in real-time. AI-based systems can detect early signs of vibration-related issues, predict impending failures, and recommend optimal maintenance strategies to prevent downtime and minimize risks. Vibration engineers can exploit AI to enhance the predictive capabilities of their monitoring and diagnostic systems, enabling proactive maintenance, condition-based monitoring, and predictive analytics.

Basic Equations for Vibration Testing

The study of vibrations and oscillations finds its expression through fundamental equations in physics.

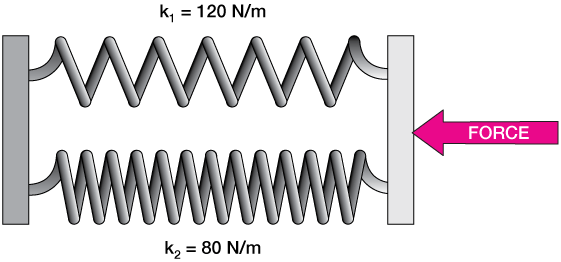
One such equation, often encountered in the analysis of simple harmonic motion, is the equation governing the displacement x=x(t) attached to a spring with spring constant k:

F = -k x

Here, F represents the force exerted by the spring on the mass, x is the displacement from the equilibrium position, and k is the spring constant.

Moreover, analyzing vibrations often involves examining the dynamic behavior of systems encapsulated by equations of motion.

For instance, in the context of a single-degree-of-freedom (1DOF) system subjected to harmonic excitation, the equation governing its motion takes the form:

m d²x/dt² + c dx/dt + k x = F_0 cos(ωt)

In this equation, c denotes the damping coefficient, F_0 denotes the amplitude of the harmonic force, and ω represents the angular frequency.

The term F_0 represents the amplitude of the harmonic force acting on the system. While this term directly denotes the force amplitude, it indirectly influences the vibration amplitude of the system's response x(t). The term ω represents the angular frequency of the external harmonic excitation. The angular frequency ω is related to the vibration frequency f (in Hertz) through the equation ω = 2π f.

With these and much more advanced equations, engineers can delve deeper into machinery's vibrational characteristics, enabling them to identify the root causes of issues and devise effective mitigation strategies.

Vibration Analysis - Is an Equation Enough?

Vibration testing remains vital for engineers despite the complexities of solving differential equations like the one above, representing a simplified model of a vibrating system subjected to external forces. Systems are often more intricate in real-world scenarios, with varying parameters and boundary conditions. Consider a suspension system in an automotive vehicle. The above equation models the motion of the vehicle's suspension subjected to external road disturbances modeled as F0 ​cos(ωt).

The system's parameters (mass m, damping coefficient c, and spring constant k) may vary due to road conditions, vehicle speed, and payload. Additionally, road disturbances may be complex and difficult to model analytically.

Here, vibration testing allows engineers to study the suspension system's response to real-world road conditions, capturing nonlinearities and variations that analytical solutions may overlook and that vibration tests can record.

Frequency Range in Vibration Analysis

Frequency range refers to the span of frequencies over which the system or component under examination is subjected to vibrational stimuli. The frequency range determines the scope of analysis and the types of vibrations the system will experience.

Expanding on this concept, the frequency range encompasses the lower and upper bounds of frequencies relevant to the particular vibration testing. These frequencies are typically defined based on factors such as the natural frequency of the system, the expected operating conditions, and the resolution during vibration testing.

The frequency range dictates the spectrum of frequencies that must be considered during the design, vibration testing, and evaluation of a mechanical system.

For example, in structural vibration testing of a building, the frequency range may span from a few Hertz (Hz) to several kilohertz (kHz), covering a wide range of vibrations induced by environmental factors, machinery operation, or seismic events.

Moreover, the frequency range influences the selection of vibration testing equipment, such as shakers and accelerometers, and the setup of test parameters, such as amplitude and duration. Different types of vibration tests, such as sinusoidal, random, or shock tests, may be conducted within specific frequency ranges to assess various aspects of the system's response.

Practical Implementation of Vibration Testing

Beyond theoretical equations, the practical implementation of vibration testing involves a structured approach. Engineers gather preliminary data, measure vibrations, interpret results, and take corrective action. This systematic methodology ensures machinery health because it facilitates interventions to maintain optimal machinery operational efficiency.

Furthermore, integrating vibration testing data into Product Lifecycle Management (PLM) systems represents a paradigm shift in maintenance strategies with the integration in the so-called "digital thread." Engineers gain insights into equipment health throughout its lifecycle by merging vibration testing results with PLM systems. This integration streamlines predictive maintenance scheduling and optimizes equipment performance while mitigating operational risks.

Moreover, by coupling vibration testing with Computer-Aided Engineering (CAE) simulations, engineers unlock enhanced collaboration and efficiency possibilities. This is a synergy between product design, testing, and maintenance teams.

Advanced Concepts - Power Spectral Density

Power Spectral Density (PSD) quantifies how signal power distributes across different frequencies in vibration testing. Mathematically, it's the Fourier Transform of the autocorrelation function of a stationary random vibration process. PSD aids in identifying dominant frequencies in machinery vibrations, offering insights into mechanical dynamics and fault detection. The core mathematical equation for the PSD Sxx(f) of a signal x(t) is:

Sxx(f) = lim(T->∞) [ 1/T * |X(f)|² ]

X(f) is the Fourier Transform of x(t), and T is observation time. Estimation techniques for vibration testing include Periodogram or Welch's method.

The PSD, denoted with Sxx(f), represents the power per unit frequency and is typically expressed in units such as m²/Hz. In simpler terms, PSD illustrates how much power is contained within specific frequency bands of a vibration signal.

In vibration testing, we collect data from vibration sensors and often obtain signals that vary over time. These signals represent the vibrations experienced by machinery and can be complex, containing contributions from various frequencies. The Fourier Transform provides a mathematical tool to decompose these time-domain signals into their constituent frequency components.

More on the Fourier Transform

Mathematically, the Fourier Transform takes a time-domain signal, such as the vibration signal collected from sensors, and transforms it into the frequency domain. This transformation reveals the amplitude and phase of different frequency components present in the signal.

In vibration testing, the Fourier Transform allows engineers to identify the signals' dominant frequencies, harmonics, and other spectral characteristics. This information is essential for understanding the underlying causes of vibrations, such as resonance or external excitation, and designing effective mitigation strategies.

Furthermore, in the context of the Power Spectrum Density (PSD) analysis mentioned in the text, the Fourier Transform calculates a signal's PSD. The PSD provides insights into how signal power distributes across different frequencies, aiding in identifying dominant frequencies and assessing the overall energy distribution in the vibration signal.

Advanced Concepts - Random Vibration Test

Alongside deterministic vibrations driven by known forces, we encounter the phenomenon of Random Vibration. This chapter elucidates the concept of Random Vibration and its implications in the context of (random) vibration testing for machinery diagnostics, building upon Power Spectral Density (PSD) analysis.

Random vibration arises from stochastic processes and is characterized by unpredictable fluctuations in amplitude and phase over time; unlike deterministic vibrations with well-defined inputs, random vibration results from inherent uncertainties or external disturbances.

Random Vibration poses unique challenges in machinery diagnostics due to its stochastic nature. It represents real-world operational conditions influenced by diverse factors such as environmental or material properties.

In vibration testing, random vibration manifests as broadband spectra with no discernible dominant frequencies. Analyzing the PSD of random vibration signals enables engineers to assess the overall energy distribution across frequency bands, aiding in fault detection and machinery health monitoring.

Mathematically, a random vibration process x(t) can be described using stochastic differential equations or through its statistical properties. The autocovariance function Rxx(τ) captures the correlation between random vibration x(t) values at different times τ:

Rxx(τ) = E[ x(t) x(t+τ)]

Where E[⋅] denotes the expected value operator. From the autocovariance function, the PSD Sxx(f) of the random vibration process can be obtained via the Fourier Transform described in the previous chapter.

How to Carry Out Vibration Testing in Practice

Vibration tests require a systematic approach, such as the one outlined in this chapter. A process is needed to evaluate the dynamic response of vibration test specimens effectively and make decisions regarding design improvements, quality assurance, and maintenance strategies.

Preparation Phase

First, we clearly define the objectives of vibration tests, including the parameters to be measured, the test duration, and the vibration test conditions. We proceed then to select appropriate vibration testing equipment such as shakers, accelerometers, and data acquisition systems based on the test requirements and the characteristics of the specimen. In the preparation phase of vibration tests, we ensure the specimen is securely mounted to the vibration test fixture to prevent any unwanted movements or resonances during testing. Consideration should be given to the orientation and mounting configuration to simulate realistic operating conditions.

Execution Phase

To conduct a vibration test, we suggest to follow the below steps:

1. Set up the vibration test equipment according to the test specifications. This includes placing and calibrating accelerometers, configuring the shaker, and connecting data acquisition systems.

2. Conduct baseline measurements to establish the initial vibration levels and verify the functionality of the vibration test setup.

3. Using the vibration shaker, apply the desired vibration test excitation profile to the test specimen. Depending on the vibration test objectives, the excitation profile may include sinusoidal, random, or swept sine vibrations.

4. Continuously monitor test conditions such as vibration amplitude, frequency, and temperature throughout the duration of the test to ensure consistency and reproducibility.

Analysis Phase

As vibration testing engineers, we capture vibration data using the data acquisition system, including accelerometer readings and any other relevant parameter, such as displacement or velocity.

We analyze the collected vibration data to assess the specimen's dynamic response. This may involve calculating key metrics such as peak acceleration, resonant frequencies, and damping ratios.

Finally, we compare the test results against predefined acceptance criteria or industry standards to evaluate the performance and structural integrity of the vibration test specimen. Identify any deviations or anomalies that may require further investigation or corrective action.

Random Vibration Testing

To initiate random vibration testing effectively, the objectives must be defined to align with the system's real-world operating conditions. This should encompass the desired input spectrum, test duration, and acceptance criteria, all of which aim to emulate realistic dynamic environments.

We must select vibration testing equipment suitable for generating and measuring random vibration signals. This equipment should include shakers, accelerometers, and data acquisition systems capable of replicating random vibration profiles accurately.

Then, our task is to develop a comprehensive test profile that mirrors the expected vibration conditions during real-world operation. We choose from various spectra types, such as Gaussian, PSD, or SRS (Shock Response Spectrum), to simulate random vibrations' unpredictable and dynamic nature accurately.

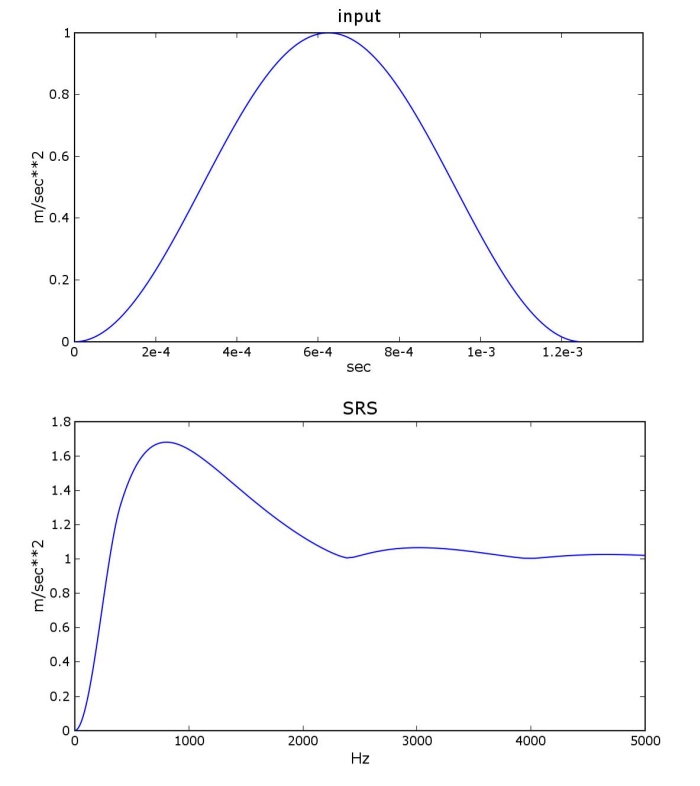
Shock Response Spectrum in Random Vibration Testing

The Shock Response Spectrum (SRS) is a graphical representation that depicts the dynamic response of a mechanical system to transient shock inputs across a range of frequencies. Unlike traditional frequency domain analyses, which focus on sinusoidal or random vibrations, the SRS characterizes the system's response to impulsive loads, such as shocks or impacts. SRS is implemented in various engineering disciplines, including aerospace, automotive, and structural engineering. Engineers utilize the SRS to assess the robustness of components and structures against shock-induced failures,

The SRS helps identify critical resonant frequencies and vibration modes that may amplify the effects of transient shock loads, leading to structural damage or failure. The Shock Response Spectrum is typically represented graphically, with acceleration amplitude plotted against frequency. Mathematically, the SRS can be derived from the response of a single-degree-of-freedom (SDOF) system subjected to an impulse or step input.

m d²x/dt² + c dx/dt + k x = F_0 δ(t)

The symbol δ(t), often called the Dirac delta function, represents a mathematical concept used in engineering and physics to model impulsive phenomena. In other words, δ(t) signifies a function that is zero for all values of t except at t=0, where it has an infinitely high and narrow peak such that its integral over the entire real line equals one. It describes an instantaneous impulse or spike occurring at time t=0, with no duration but possessing a finite area under the curve. This mathematical abstraction is advantageous in representing idealized point loads, such as sudden impacts or impulses, in various dynamical systems and differential equations.

Random vs Sine Testing

Random vibration testing and sine vibration testing are two common methods for assessing the dynamic response and structural integrity of mechanical systems.

In random vibration testing, the excitation signal consists of a broad spectrum of frequencies with varying amplitudes, simulating real-world operational conditions where the input forces are unpredictable and stochastic in nature. This method is beneficial for assessing the robustness of a system against vibrations encountered in everyday use, such as those caused by road conditions, machinery operation, or environmental factors like wind and waves. Engineers analyze the PSD of the random vibration signal to understand how the energy is distributed across different frequency bands. This helps identify resonant frequencies, assess structural damping, and detect potential weaknesses or fatigue issues in the system.

Sine Testing

On the other hand, sine testing applies a single-frequency sinusoidal excitation signal to the system, typically at varying amplitudes or frequencies to characterize its response under different conditions, hence the name of "sine testing". This method is commonly used for modal analysis, where engineers seek a structure's natural frequencies, damping ratios, and mode shapes. Sine testing is also employed for durability testing, where components are subjected to repeated sinusoidal vibrations to assess their fatigue life. Engineers analyze the FRF of the system, which describes its dynamic response to sinusoidal excitation across different frequencies. This allows them to determine resonant frequencies, modal parameters, and frequency-dependent damping characteristics.

In summary, random vibration testing mimics real-world vibration conditions with a broad spectrum of frequencies, making it suitable for assessing overall system performance and durability. Sine vibration testing, on the other hand, focuses on characterizing specific dynamic properties of a system through controlled sinusoidal excitation. Both testing methods complement each other and are valuable tools in the vibration analysis toolbox, depending on the specific objectives and requirements of the testing scenario.

In summary, a vibration testing system is a crucial apparatus used to subject test specimens to controlled vibrational inputs. These inputs typically involve applying harmonic, random or swept sine vibrations to simulate real-world operating conditions. One essential aspect of a vibration testing system is its ability to ensure that all components of the test specimen vibrate at the same frequency. This synchronization is vital for accurately replicating the dynamic environments encountered by machinery during operation.

Advanced - Frequency Response Function (FRF)

During vibration testing, engineers measure the specimen's response, such as acceleration or displacement, while applying harmonic excitation across a range of frequencies. The FRF is then obtained by taking the ratio of the output response to the input excitation at each frequency.

The FRF provides crucial information about the system's natural frequencies, resonance peaks, damping ratios, and amplification factors. Engineers can analyze the FRF to identify resonant frequencies, assess damping characteristics, and evaluate structural integrity. Moreover, the FRF aids in validating analytical models, calibrating simulation parameters, and optimizing design parameters to meet performance requirements. The FRF is mathematically represented as the ratio of the system's output response to the input excitation in the frequency domain.

Denoted as H(ω), where ω represents the angular frequency, the FRF is expressed as:

H(ω)=F(ω)/X(ω)​

where X(ω) is the Fourier Transform of the system's output response, and F(ω) is the Fourier Transform of the input excitation.

‍