What are the challenges in F1 Engineering? Which technologies are behind successful teams, and what’s next? How many of these technologies can be adopted by mass production cars we drive daily?

We will explore the role of aerodynamics in F1 car design in its various aspects: how the surrounding airflow interacts with the F1 car aero appendages, the importance of measuring approaches in wind tunnels, what are “FIA Regulations” and finally, what are the roles of CFD (Computational Fluid Dynamics) and AI (Artificial Intelligence).

AI in the automotive industry is starting to play a decisive role in making design teams more competitive with simulation tools. It is considered even more so in an environment such as F1. Due to space reasons, we will only touch on practical subjects such as rear ride heights, aerodynamic configuration or theory boundary layer theory in CFD. We will conclude with a Use Case of AI applied to simulating a front wing + front tires' geometry with turbulent air conditions.

Why More Downforce Is Needed in F1 Cars Aerodynamics

Aerodynamics optimization is crucial in Formula 1, making the difference during a race. F1 racing circuits are designed to be challenging for drivers and exciting for spectators. Tracks typically feature a combination of straightaways for top speed, tight turns, and elevation and surface type changes. Some circuits are designed to be more technical, with many tight turns, while others are designed to be more high-speed, with long straightaways and faster turns.

Therefore F1 car should be fast (as everyone imagines). F1 cars are not designed like “cigars” for an ideal streamlining and have many appendages.

How so?

To navigate the tight turns and complex layouts of the circuits they race on, F1 cars need to be manoeuvrable. Many devices and technologies can improve the manoeuvrability of an F1 car: aerodynamics is not only about overcoming air resistance (better drag) but also making the F1 car more adherent to the track floor.

In summary, the car body and its appendages, such as the rear wings and the front wing group, are usually thought to be “streamlined”. But what is essential is that the F1 car and appendage shape create more “downforce”.

Downforce is crucial as it allows an F1 car to generate extra grip and maintain stability at high speeds. This is achieved by designing the car’s bodywork to create a downward force on the car as it moves through the air.

Downforce helps to press the tires onto the track, increasing the amount of traction available to the driver and allowing them to take corners at higher speeds. Additionally, the downforce also helps to improve the F1 car’s stability, making it more difficult for the vehicle to spin out of control. This is critical in a sport where race cars can reach speeds above 300 km/h!

How to Measure Downforce? Traditional Aerodynamic Testing

Traditionally, prototypes of vehicles were built and tested in wind tunnels to measure downforce with aerodynamic testing. It is important to note that teams keep their measurement methods and data privacy, as they are part of the F1 car’s performance secrets.

One standard method is to use a load cell, a device that can measure the weight or force exerted on it. The load cell can be placed under the car and used to measure the force generated by the car’s downforce. Another method is to use a balance beam, a device that can measure the weight or force exerted on it by suspending the vehicle from it and measuring the deflection of the beam.

Another way of measuring downforce is using a Pitot tube. A Pitot tube is a device that measures the pressure difference between the front and back of the car. This can be used to calculate the downforce being generated by the car.

How to Measure Downforce? Traditional CFD

From the 90s, wind tunnel testing started to be assisted by 3D engineering computations or CFD (Computational Fluid Dynamics).

In today’s teams, engineers rely on high-fidelity numerical aerodynamic simulations (i.e. CFD) to assess the effect of design variations without actually building the prototype and going to wind tunnel testing.

Measuring downforce using CFD typically involves creating a digital model of the F1 car and its surrounding environment, such as the track and other vehicles. The model includes boundary conditions such as the simulated velocity and wall roughness and state-of-the-art computational meshes. The model is then used to simulate airflow around the car and calculate the aerodynamic forces acting on it. This can include the amount of downforce generated.

It is important to note that a CFD F1 simulation will not run on a desktop computer!

It’s Much More Than Increasing Downforce!

For the sake of space, we have focused on downforce, its measurement and its computation. However, other aerodynamic phenomena are relevant.

Wake structures. The wake of a car in front of another vehicle can reduce the aerodynamic drag on the next vehicle. This is one of the reasons why drafting, or following closely behind another vehicle, can be an advantage in Formula 1 racing. When a vehicle is following closely behind another vehicle, the airflow over the following vehicle’s front wing is disrupted, reducing the amount of downforce generated by the wing and the drag on the car. This can allow the next car to travel faster than it can. However, the wake can also disrupt the airflow over the rest of the car and make it more difficult for the driver to maintain control in the so-called dirty air. The advantage of drafting is balanced by the increased difficulty of driving in the wake.

CFD Technology Overview

The Navier-Stokes equations are at the core of all fluid processes, including aerodynamics:

∂u/∂t + u · ∇u = -(1/ρ) ∇P + ν ∇²u

The Navier-Stokes equations are a set of mathematical equations, including fluid velocity u, fluid pressure P and density ρ, that describe (with other equations and several assumptions) the motion of fluids. These and other equations are based on mass, momentum, and energy conservation laws.

Now for the bad news; there is no general analytical solution to the Navier-Stokes equations. In general, solutions to the equations require numerical approximations such as CFD. CFD can yield the fluid’s velocity, pressure, and temperature at different points of three-dimensional space included in the simulation domain. The Navier-Stokes and other equations can be translated into CFD in several ways; the most common method is the finite volume method.

The integral (“∫ ") form of a conservation equation for quantity “φ” (φ can be momentum or energy, etc.) is expressed as follows:

∫ ∫ ∫ ∂φ/∂t dV + ∫ ∫ (Flux of φ) dS = ∫ ∫ (Source Term of φ) dS

where “V” is the control volume, “S” is the surface of the control volume, “Flux” is the flow of the variable through the surface, and “Source Term” is any other term that can affect the variable within V. Assuming the problem is steady-state and incompressible, the “∫ “over continuous domains become”∑“over computational discretizations (discretized volumes) and:

∑ (Flux_i A_i) = ∑ (Source_i A_i)

Here, Flux_i is the flux through a discretized volume’s face numbered “i”, A_i is the area of the face i, and Source_i is the source term in computational cell “i”. This equation represents the conservation of mass for each computational cell (a discretized volume).

How does the variable φ change from one cell “i” to another? A simple numerical approach is called an “Upwind Scheme”. The upwind scheme uses the fluid velocity direction to determine the spatial derivatives’ direction. The scheme is called “upwind” because it uses the flow variable value at the position upstream “i-1” of the current position “i” to approximate the derivative. This is a way to approximate the spatial derivatives in the Navier-Stokes equations.

From an operative point of view, the process of translating the Navier-Stokes equations into CFD using the finite volume method can be summarised as follows:

1. Discretize the model: Divide the model into many small, manageable cells, known as a mesh. This allows the computer to calculate the fluid flow within the model.
2. Approximate the equations: The Navier-Stokes equations are approximated at the cell centres; this process is called spatial discretization. The equations are written in terms of the average values of the properties in each cell.
3. Boundary conditions: The solution obtained from the numerical method is subject to the boundary conditions, which are the conditions the fluid must satisfy at the boundaries of the simulation.
4. Numerical solution: The algebraic equations resulting from the spatial discretization are solved using iterative numerical methods.

The FVM is a widely used method in CFD; it is relatively simple to implement and can handle complex geometries and boundary conditions. However, it is not the only method available.

What are the CFD resources needed to simulate aerodynamics in F1?

The hardware used to run CFD simulations in motorsport is typically high-performance computing (HPC) systems. These systems are designed to handle the large computational workloads and data storage requirements of CFD simulations.

The main components of an HPC system used for CFD in Formula One racing include at least the following:

• Servers: These are the central computational units of the system and are responsible for running the CFD simulations. They typically consist of multiple processors (thousands or tens of thousands) and a large amount of memory. Servers also have high-speed interconnects to facilitate fast data transfer between the different computational nodes.
• Storage: CFD simulations generate large amounts of data, so the HPC system needs a high-performance storage solution to store and manage this data. This can include network-attached storage (NAS) systems, parallel file systems, or object storage systems like S3.
• Cluster Management Software: To manage the resources of the HPC system, cluster management software is used. Examples are Slurm, PBS and LSF. This software is responsible for scheduling jobs, allocating resources, and monitoring the system’s status.
• Powerful Visualization: To analyze the results of the CFD simulations, teams typically use visualization software, such as ParaView, Tecplot, and Ensight. This software can display CFD results in various formats, such as 3D images and plots. It can be used to analyze the aerodynamic performance of the car.
• License management and advanced CFD tools: CFD software is typically commercial and requires a license to run. Formula One uses license managers such as FlexLM, RLM and LUM to manage the licenses and ensure that the team uses the software within the terms of the license agreement.

All these HPC systems run on Linux operating systems and are often integrated with the team’s data management and analysis systems.

It’s also worth noting that Formula One teams have a very high standard regarding security, as they want to protect their data and intellectual property. Therefore, they often use specialized security software to secure their HPC systems, such as firewalls, intrusion detection systems, and VPNs.

A Bit of Engineering: Role of Rear Wing and Front Wing

Let us review the basics of F1 aerodynamic development. The rear wing’s design is a critical aspect of Formula One aerodynamics, as it can significantly impact the car’s performance via rear downforce.

The rear wing works by diverting the air stream over the race car in such a way as to create a low-pressure area on the top surface of the wing and a high-pressure area on the bottom surface. This creates a pressure difference between the top and bottom of the wing, which generates a downward force.

The rear wing comprises several elements, including the main plane, the endplates, and the rear wing flap(s). The main plane is the primary surface of the wing that creates the majority of the downforce, while the endplates are used to guide the airflow over the wing and control the pressure distribution. The flaps can be adjusted to fine-tune the downforce and drag balance of the car and are a crucial component in the car’s setup.

The rear beam wing (RBW) is a specific car rear aero structure. RBW is a type of aerodynamic device mounted on the rear of the car, typically a narrow and high wing above the rear suspension and parallel to the rear axle. It is designed to generate downforce and improve the car’s handling and stability at high speeds.

The rear beam wing works by redirecting the airflow, air passing over the rear of the car and creating a high-pressure area above the wing and a low-pressure area below it. Pressure differences produce downforce. The aero importance of the RBW is that it plays a crucial role in improving the car’s aerodynamic balance. The RBW also helps reduce the drag coefficient on the car, making it faster and more efficient. Reduce drag coefficient helps on straightaways.

The front wing is another key component creates aerodynamic downforce. The front wing is typically located at the front of the car and is designed to create a downward force on the car as it moves through the air. This force helps to press the front tires into the track, increasing the amount of traction available to the driver and allowing them to take corners at higher speeds. Additionally, the downforce also helps to improve the car’s stability, making it more difficult for the car to spin out of control.

The front wing works by diverting the airflow over the car in such a way as to create a low-pressure area on the top surface of the wing and a high-pressure area on the bottom surface. This creates a pressure difference between the top and bottom of the wing, which generates a downward force.

Which one is the most important between the rear wing and front wing ?

Both the rear and front wings are essential components of Formula One!

• The downforce produced by the front wing is essential for providing traction to the front tires and allowing the driver to take corners at higher speeds.
• The downforce due to the rear wing is essential for providing traction to the rear tires and maintaining the car’s stability at high speeds.

It is difficult to say which one is more important for creating downforce in Formula One, as both the front and rear wings play a critical role in the car’s performance. The front wing and the rear wing are designed to work together, and the downforce produced by each wing is dependent on the other wing.

However, the rear wing is generally considered more critical for generating downforce in Formula One. The rear wing is typically larger than the front wing and generates a greater proportion of the car’s total downforce. Additionally, the rear wing is typically more adjustable than the front wing, which allows teams to fine-tune the car’s aerodynamic performance. The rear wing is also subject to more regulations than the front wing regarding size, shape, and number of elements. Therefore, its engineering is even more challenging.

Over the course of the years, the distribution has changed; in the 1990s, the average F1 car produced 40-50% of its total downforce from the front wings and 50-60% from the rear wings. Recently, the average F1 car produced around 30% or less of its total downforce from the front wing and 70% or more from the rear wing.

Method Overview: From Wind Tunnel Testing to AI

Fluid Dynamics simulations are at the heart of the car development process of all Formula 1 teams and one of the critical performance factors for the race. Even though teams can generate thousands of simulations annually and explore as many design variations, they are limited both by the computational cost and the rules from the FIA (International Automobile Federation). Among this large number of designs, it is critical to converge quickly towards designs corresponding to a reasonable compromise. Hence, running fast simulations can be critical in this phase. However, low fidelity simulations are not an option since the very complex nature of the phenomena can only be captured with high-fidelity resolution.

Engineering computations require a high degree of accuracy since the slightest improvement can impact aerodynamic performance. Also, simulations need complex mathematical operations over (hundreds of) millions of points in 3D space. This can only happen with massive RAM and big numbers, up to thousands, of processors such as CPU or GPU.

Summary - Pros of CFD Compared to the Wind Tunnel Model:

• time from prototype to wind tunnel testing
• repeatability of tests
• integration with design (CAD)
• associated costs for materials, transportation, storage

Summary - Cons of CFD:

• skills required to run a computation are not for everyone and go beyond reading the software handbook, especially in F1
• the speed of computations (and timeliness of delivery of results) only comes at a cost; the cost is a big HPC cluster
• There is no real full integration with designers and their tools: the designed CAD is the material car. However, CFD requires an aerodynamic abstraction (“CAD Cleaning”)

Now we come to the question, could AI help CFD and can AI help F1 teams?

It is now acknowledged that AI is digitalizing the automotive industry. Is there a way to introduce AI into aerodynamics by reducing the complexity of CFD calculations for F1 aero without losing accuracy?

Let us first review a few traditional AI approaches.

• Kriging is a method to predict unknown values at a given point using the known values of surrounding points. The prediction is based on a spatial correlation model. Kriging is commonly used in mining and all fields where spatial data are collected.
• Surrogate modelling via Gaussian Process (GP) Regressors is a method of creating a simplified model of a complex system. The simplified surrogate model predicts the complex system’s behaviour without running the full system. GP Regression is a non-parametric Bayesian method for fitting a smooth function to data. Bayesian inference uses prior knowledge and data to infer probability distributions of model parameters. GP regression models the function as a Gaussian distribution and uses the system data to infer the underlying distribution's parameters. The formula is: y ~ GP(m(x),k(x,x')), where: y are the target values, x are the inputs, m(x) is the mean function and finally, k(x,x') is the similarity/covariance between the input variable x and x'.

• Reduced Order Modeling (ROM) encompasses methods to create a simplified mathematical model (surrogate or ROM) of a complex system, reducing the cost and time of simulating it in full detail. a ROM can provide surrogates for 3D CAE simulations. ROM encompasses a variety of methods for creating reduced-order models, such as POD Proper Orthogonal Decomposition).

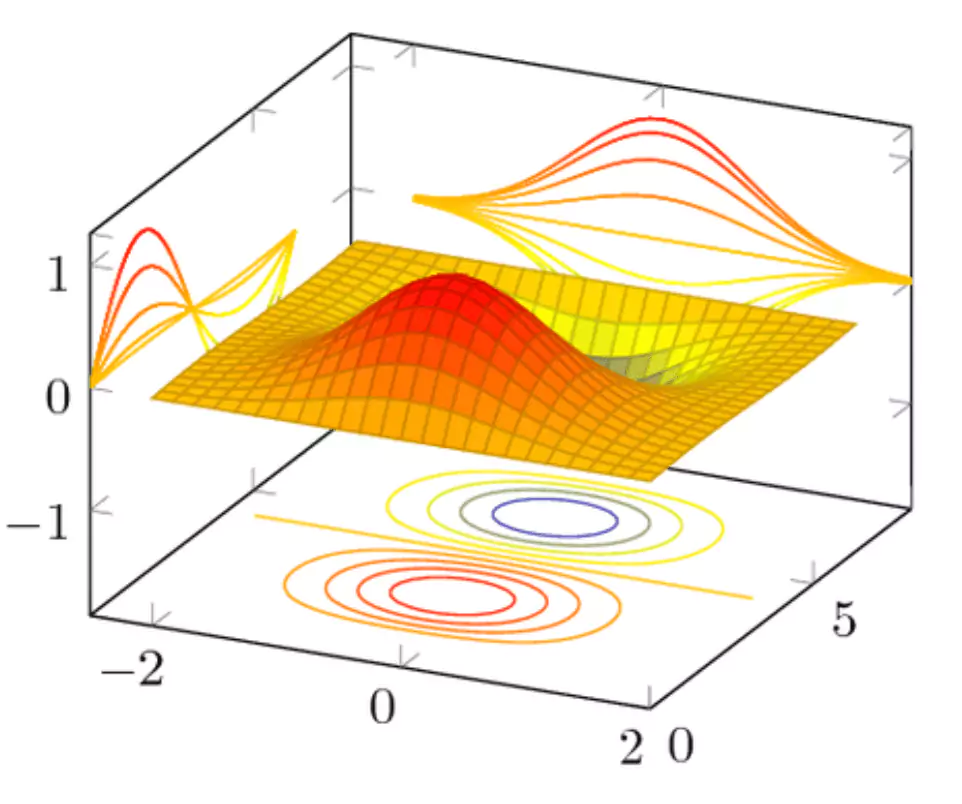
What are the limitations of ROM? When creating a ROM, parametrization creates a reduced-order model for predictions. However, this model is only valid for the specific parametrization used to create it. If the parametrization changes, the reduced order model may no longer be accurate, and a new reduced order model will have to be created. Also, for non-linear systems, the range of the parametrization where the model can be used with reasonable accuracy must be carefully evaluated.

There is a felt need for more advanced approaches than ROM.

The automotive industry has shown benchmarks of geometric deep learning vs Gaussian processes for aerodynamic use cases.

Novel AI Approaches From Neural Concept

Neural Concept Shape (NCS) opens the door to a solution to this problem through Geometric Convolutional Neural Networks (CNNs).

A convolutional neural network is an artificial neural network commonly used in image processing.

From One to Thousands of Aerodynamic Configurations per Day

In this project, our application engineers evaluated the performance of NCS Projective Regressor Neural Network model (a model that projects high-dimensional data into a lower-dimensional space).

Engineers focused on the front side of the vehicle, from the front wing to the bargeboard, including the nose of the car.

Data for this project are a simplified version of the more complex and confidential data found in operational conditions in Formula 1. Several practical F1 challenges were considered, including long-range interactions, complex vortex structures, multiple connected components and the importance of geometrically fine details.

F1 Use Case

F1 Use Case: Generative CAD Design

In this case, we could not utilize the source F1 data from a real F1 team for obvious confidentiality reasons. We resorted to dataset synthesis.

• Dataset synthesis generates new data samples similar to existing ones but with variations. This can be done by simulating the underlying processes that generated the original data. The goal of dataset synthesis is to increase the size and diversity of a dataset to train the neural network or even to create a brand new dataset, as in our case.

Onshape CAD was used to design the car geometry by varying up to 56 different variables, as detailed in the figures (parameters description).

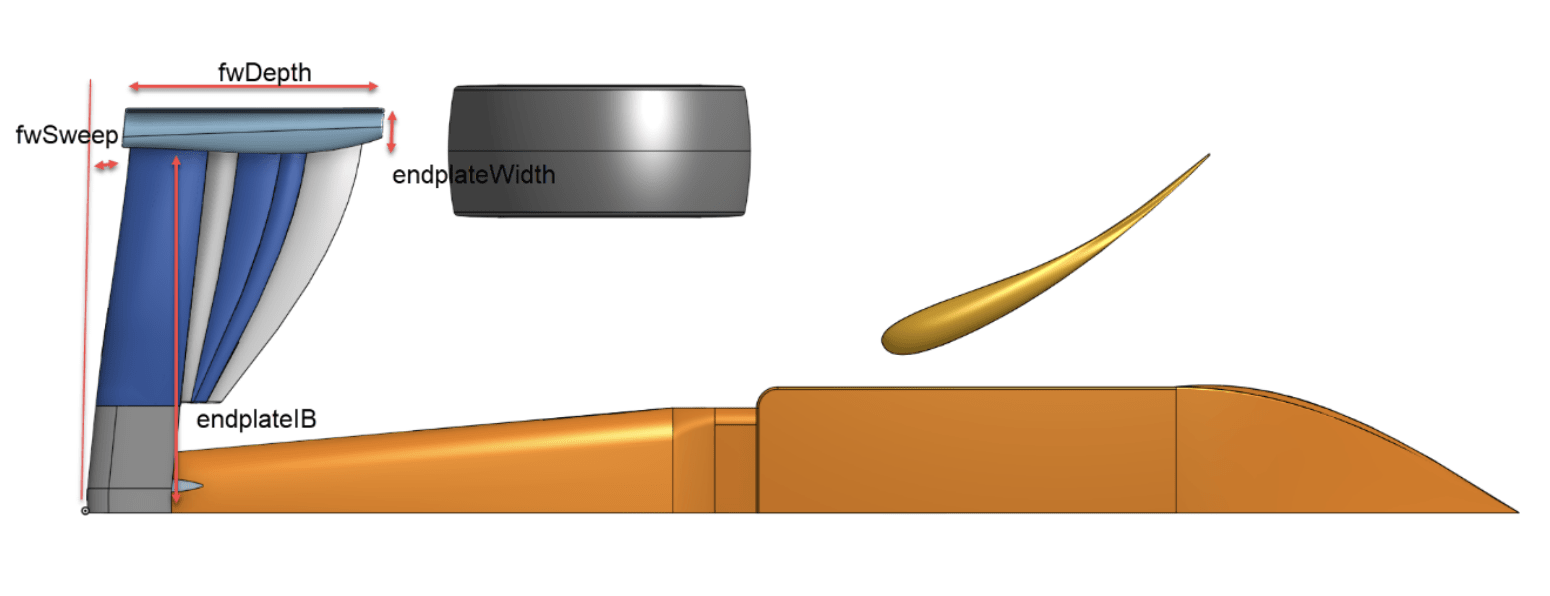
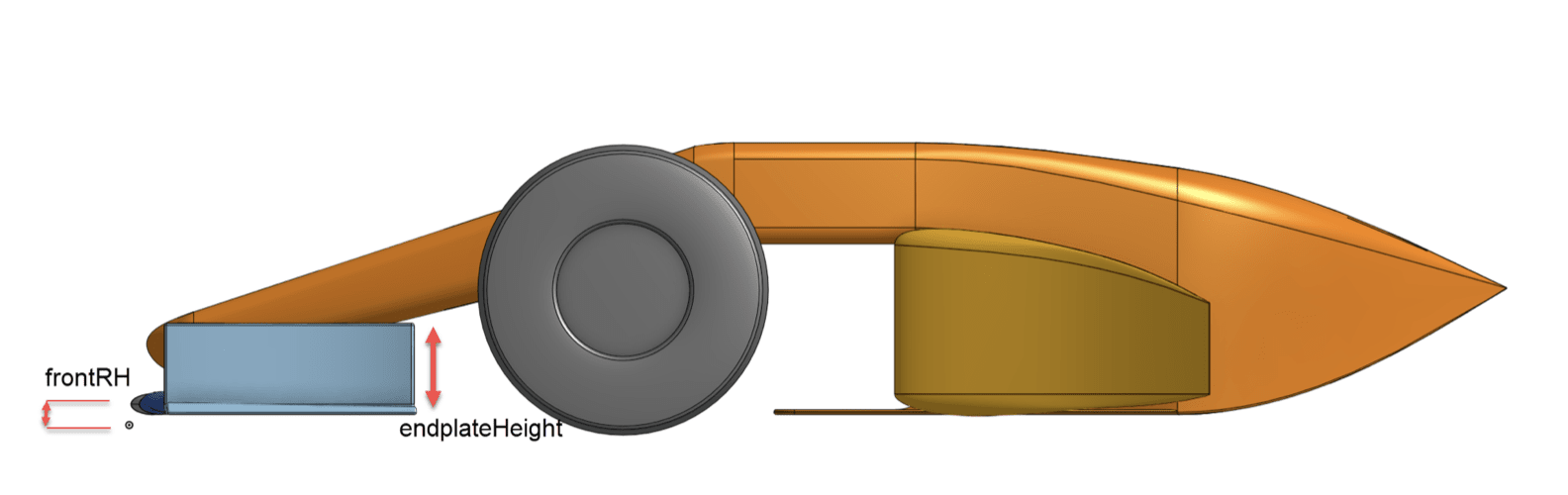
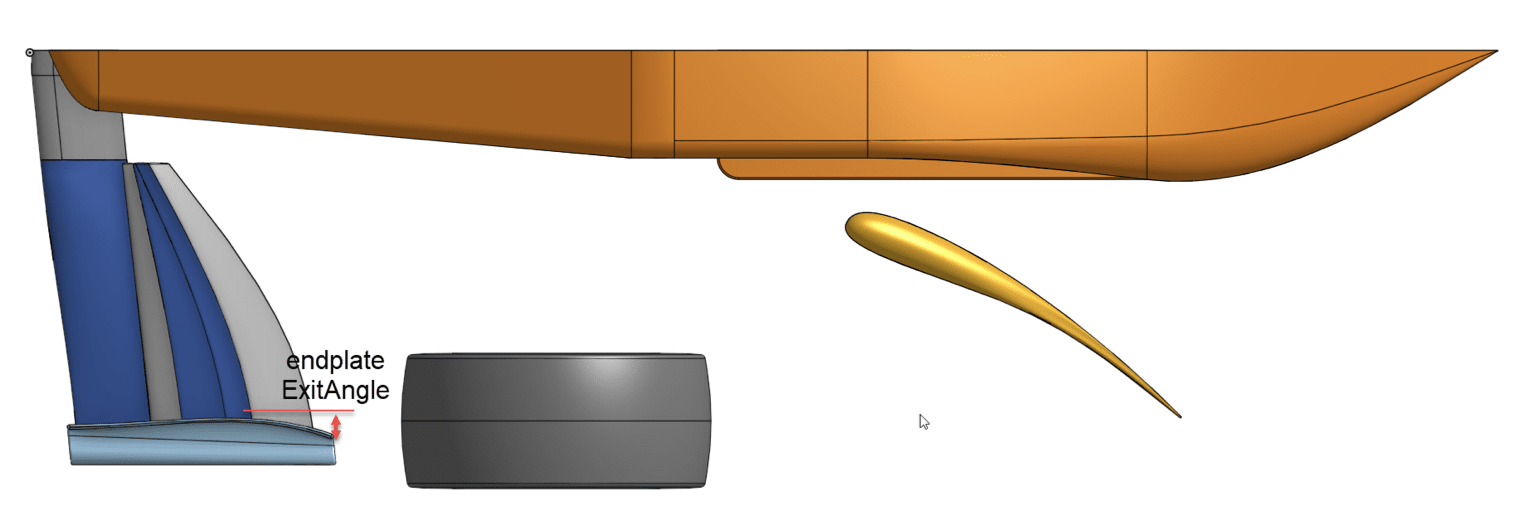
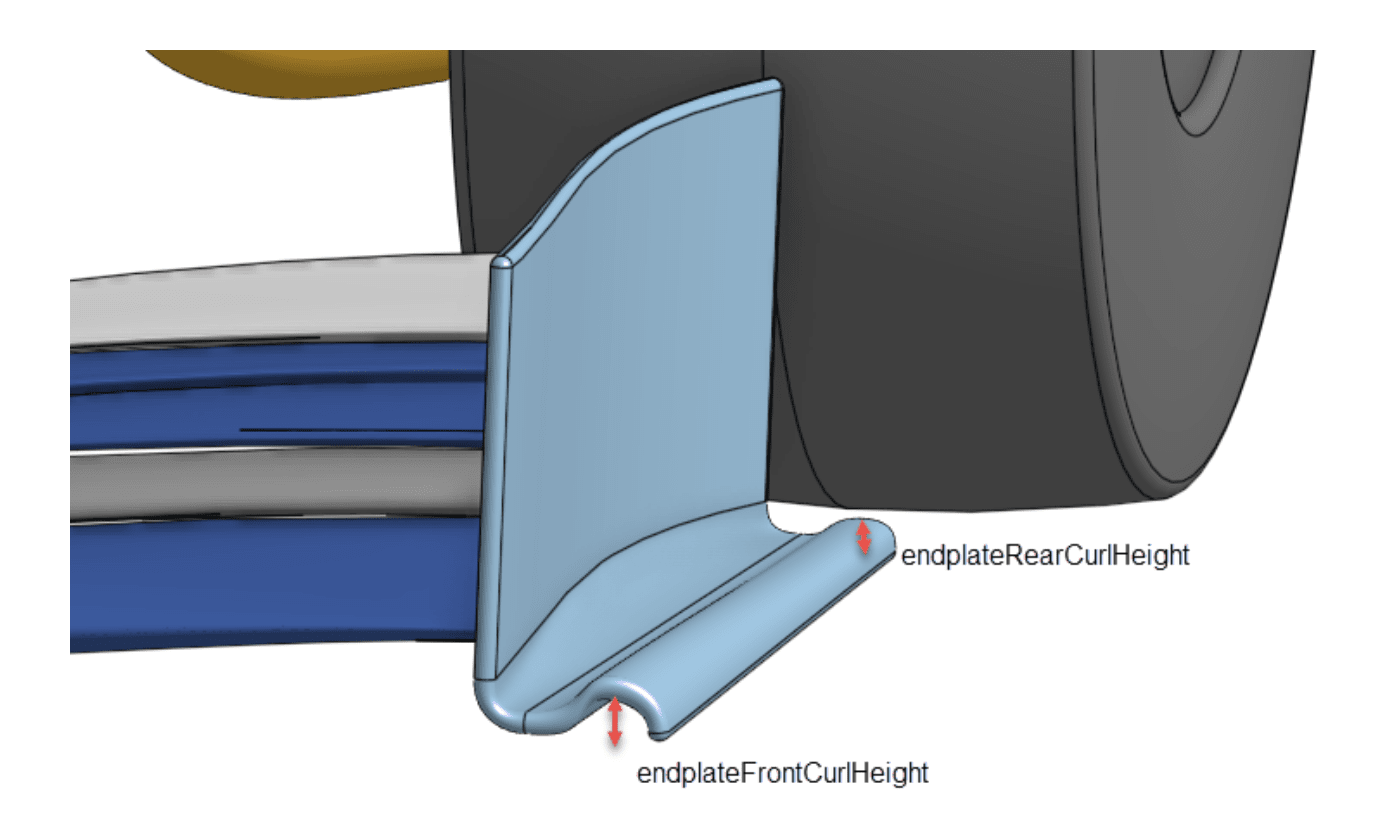
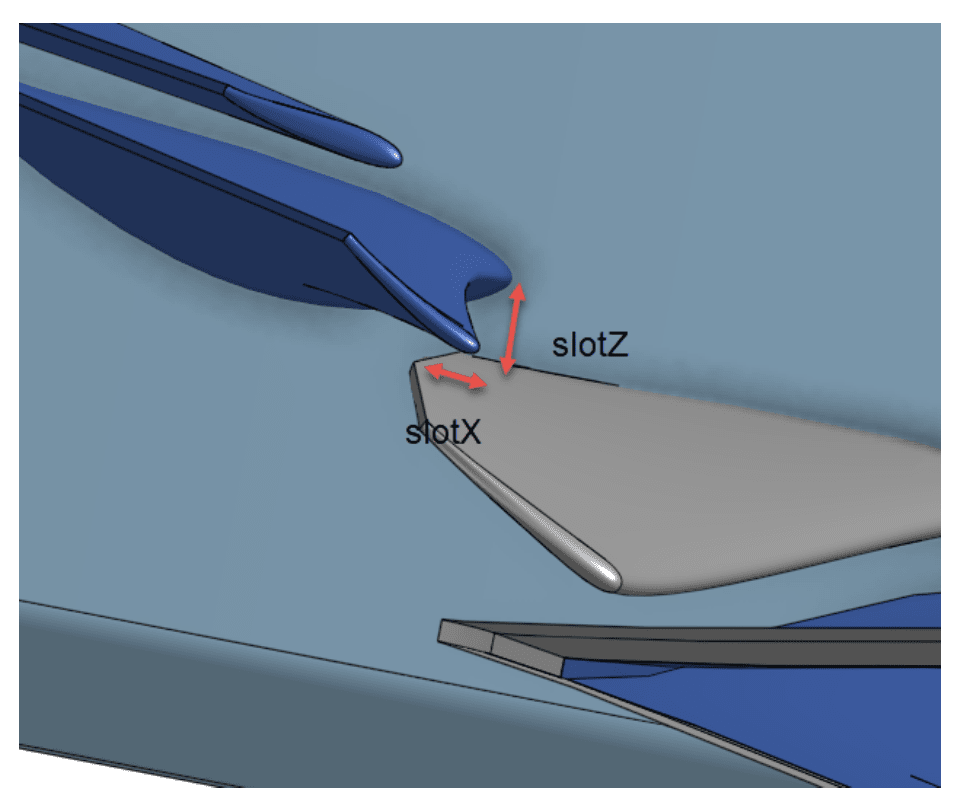
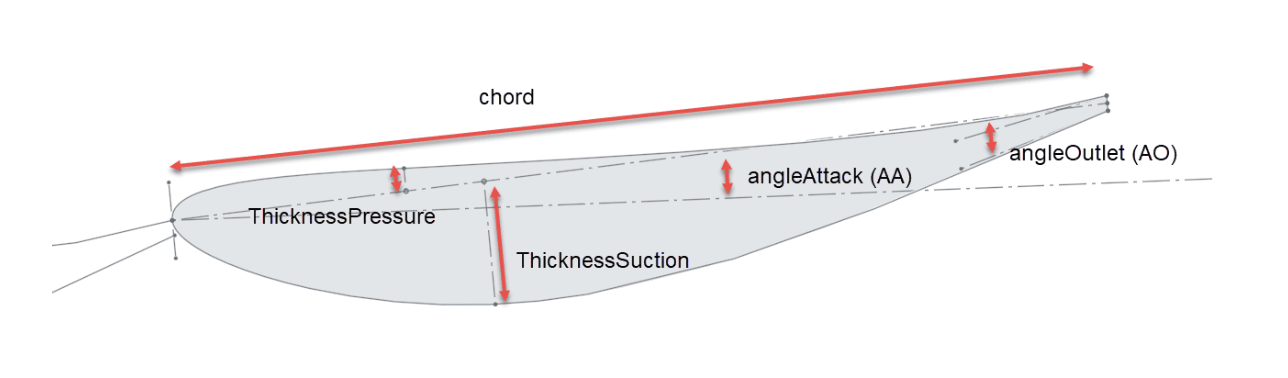
This allowed performing fine design variations on the car. Defining lower and upper bounds for each shape parameter, a random value was chosen at each iteration. Thus, we built a database of 1644 geometries that ensured a good distribution, each being unique in the dataset.

Onshape geometries were exported as STLs. This CAD format expresses a more realistic non-parametric nature and s representative of the difficulties that NCS can easily overcome while ROM cannot tackle.

F1 Use Case: Numerical Simulation

OpenFOAM was used for CFD simulations at 250 km/h (70 m/s) velocity without crosswind. We used half of the car (symmetry). The tire was defined as rotating according to the car’s speed.

It was essential to take into account turbulence modelling.

Turbulence affects car aerodynamics: flow can form vortices and other structures that disturb airflow across wings and other aerodynamic devices, diminishing their effectiveness and making it harder for the driver to manage the car.

The turbulence model used was SST k-ω transport: it uses two equations to describe the turbulent flow of a fluid, and it is considered a Reynolds-Averaged Navier-Stokes (RANS) model. It is widely used because of its ability to predict flow features in complex geometries, such as in F1.

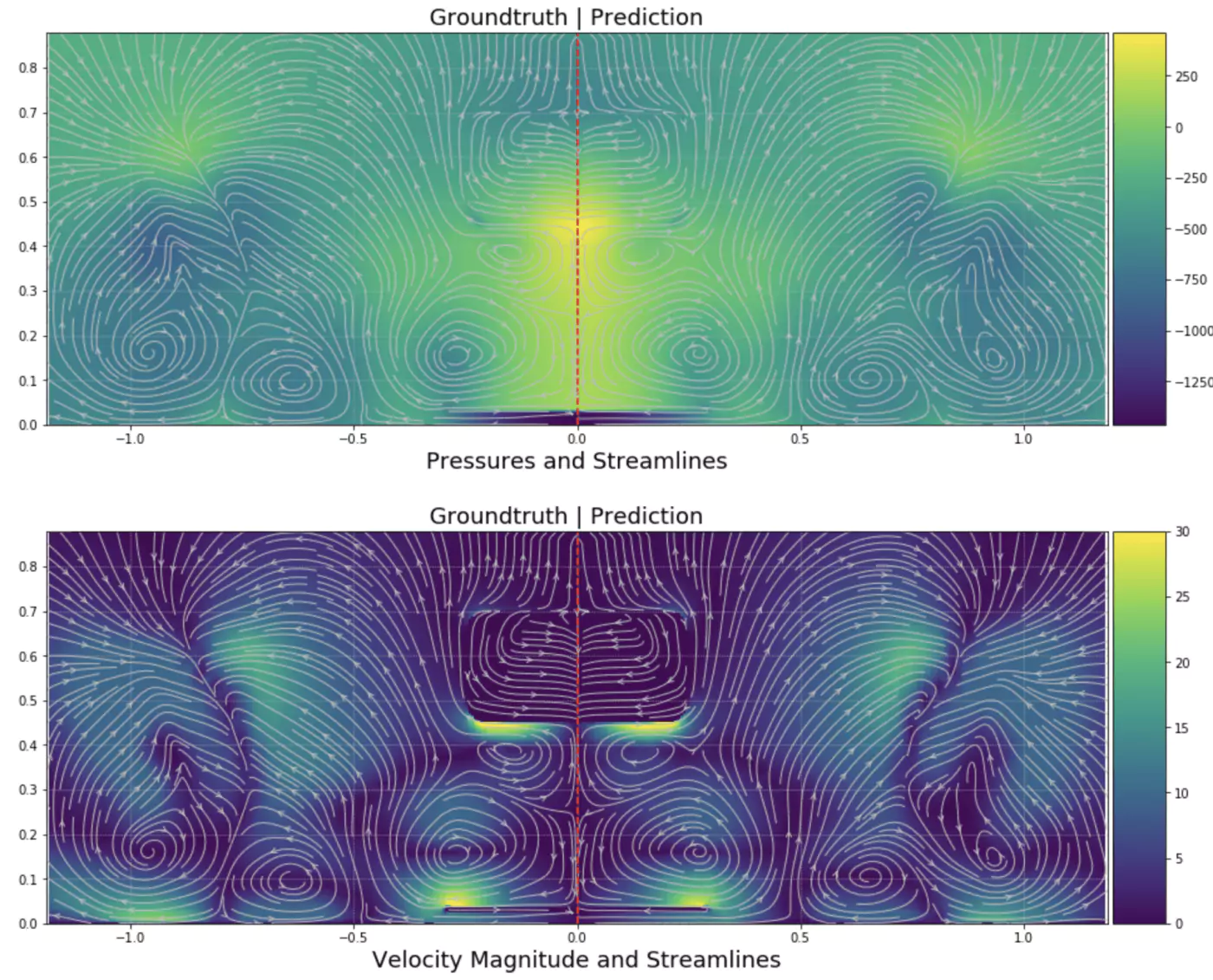
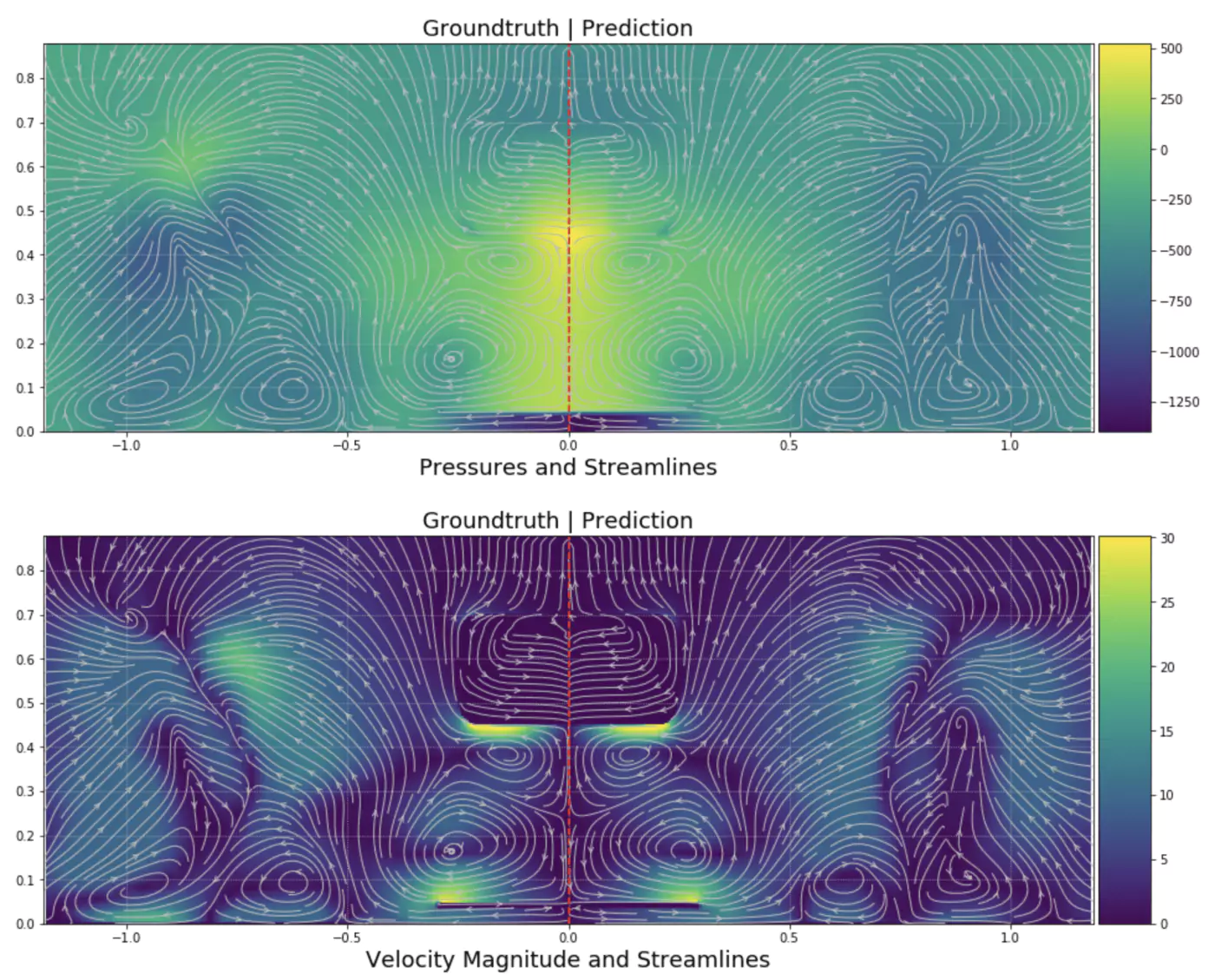
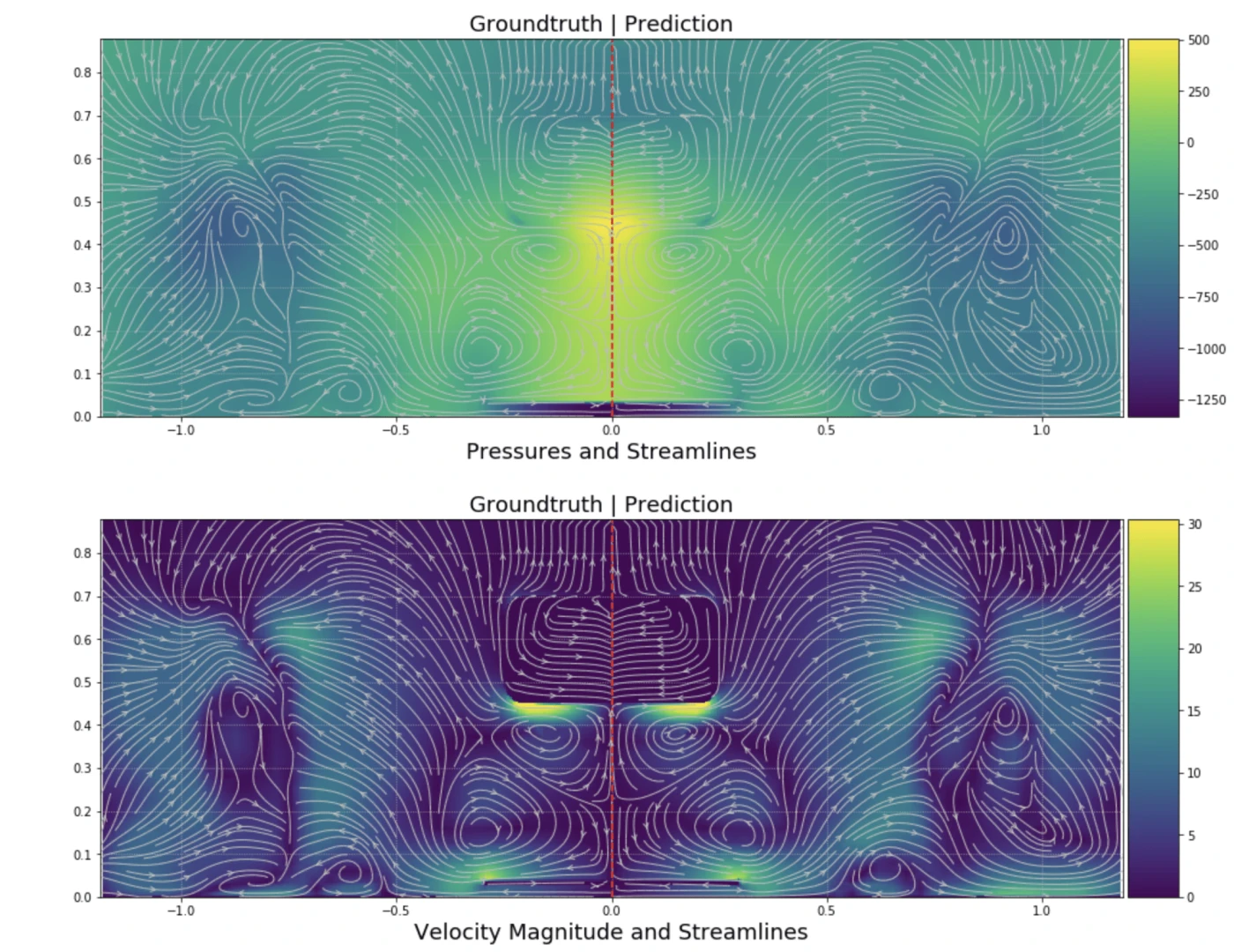
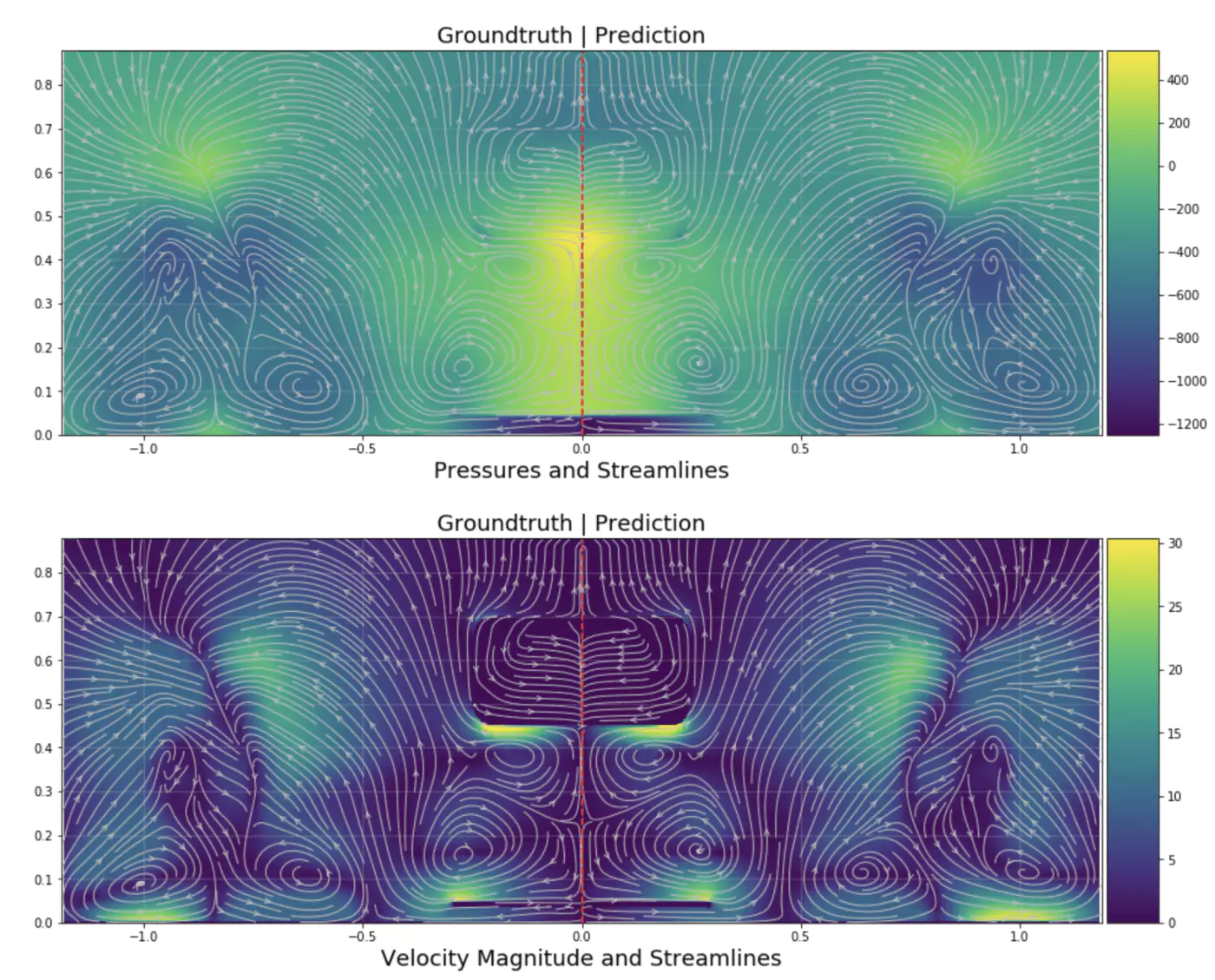
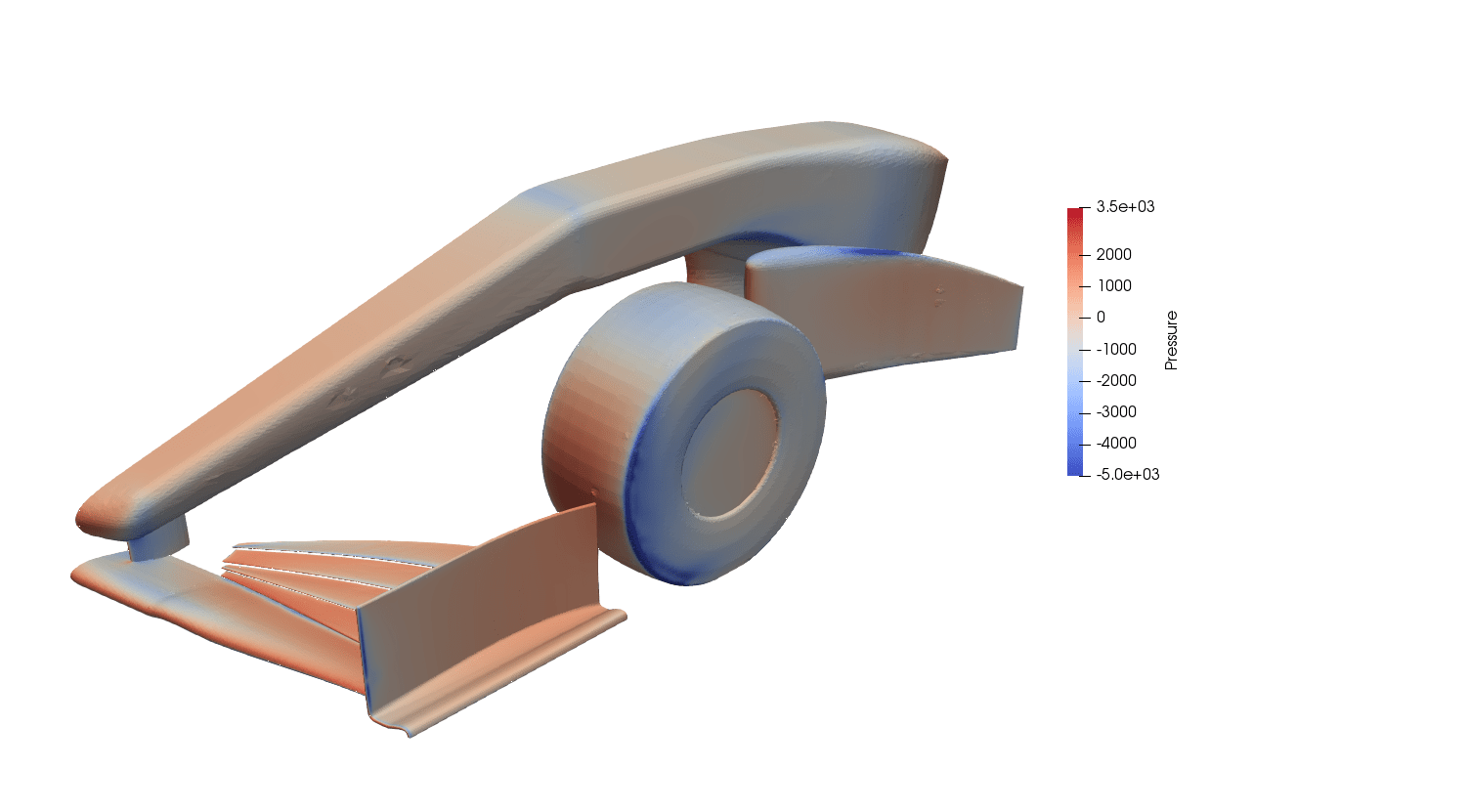
Simulation postprocessing was extracted on the car’s surface, as shown in the figure.

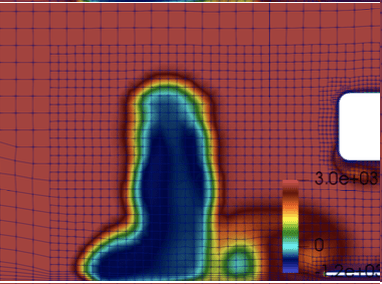
The flow field has also been visualized on a plane slice taken at the last iteration of flow field at 1.7 m, i.e. just behind the tyre. These data were used to train the deep neural network. Indeed, usually, taking the whole 3D volumetric prediction is too expensive for high-fidelity simulations. Hence, using plane slices is a good trade-off and allows us to more precisely assess the influence of slight geometry variations. This vertical plane slice also allows us to observe some critical flow phenomena along the car that aerodynamicists wish to control. A visual example is given in the figure.

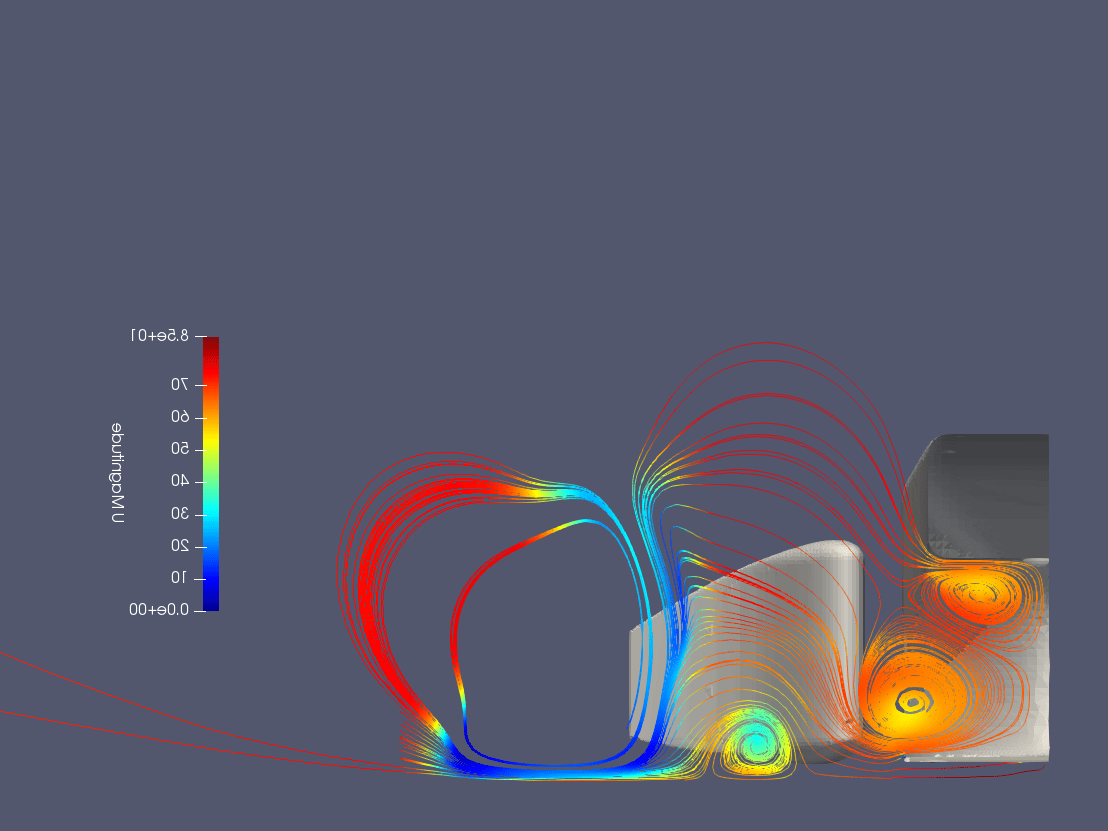
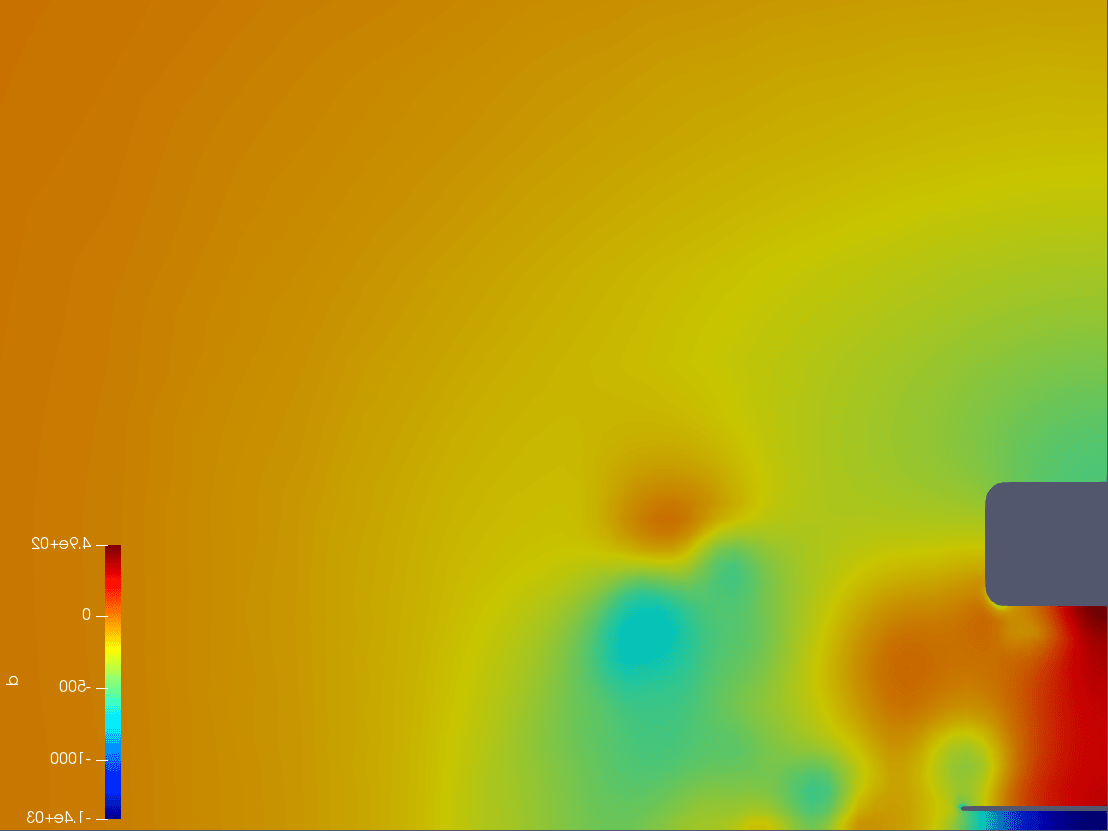
The vertical plane is just behind the tyre in which vortexes are present.

Note that the neural network is unaware of the underlying parametrization: only the similarity to the shape present on the training set will have an effect on the accuracy.

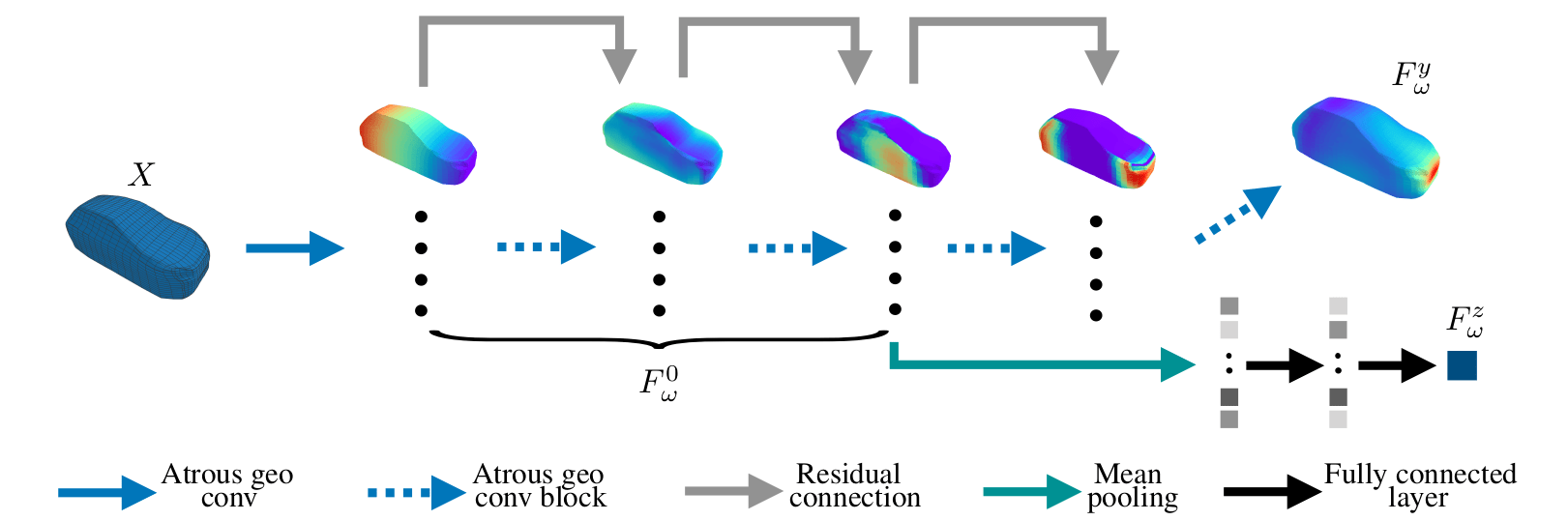
Convolution on the shape is illustrated below.

• The first branch pre-processes the input and constructs a set of features using the previously introduced geodesic convolution operations. These features predict the global scalars via average pooling and two dense layers.
• The second branch of the network generates pressure fields relying on an additional set of geodesic convolutions and point-wise operations. The new network exploits GPUs for efficient implementation of geodesic convolutions.

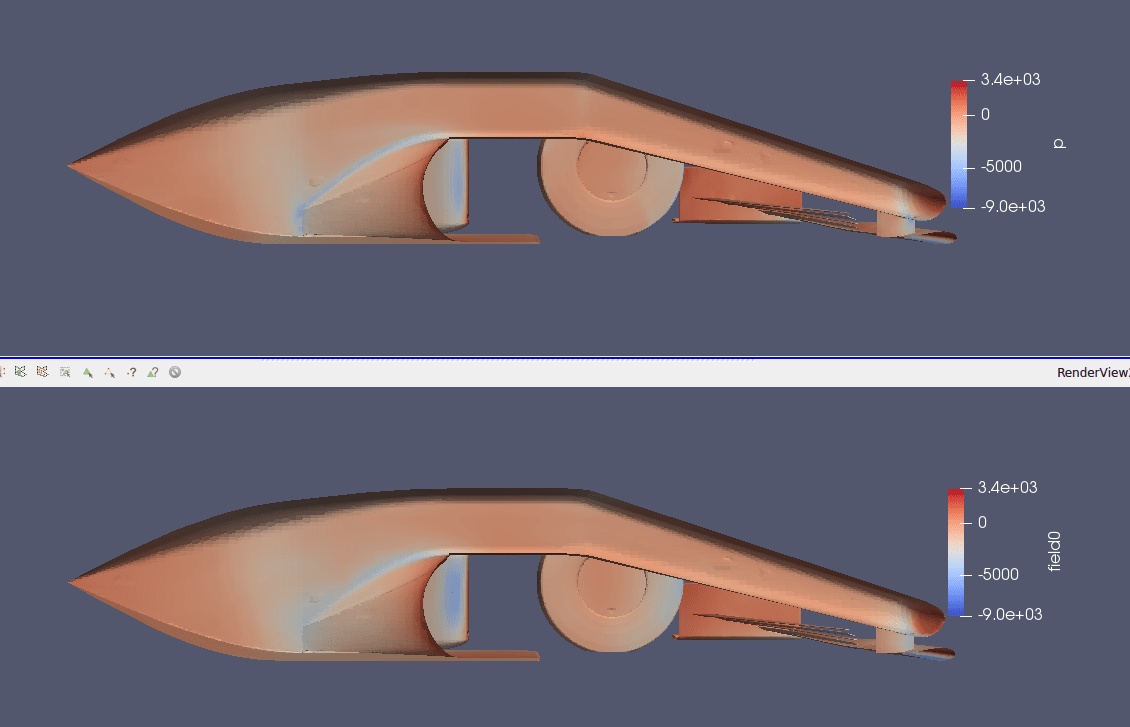
First, we predicted the flow on the car’s surface and evaluated the aero performance. The solution on the car’s surface is relatively robust to the changes in shape.

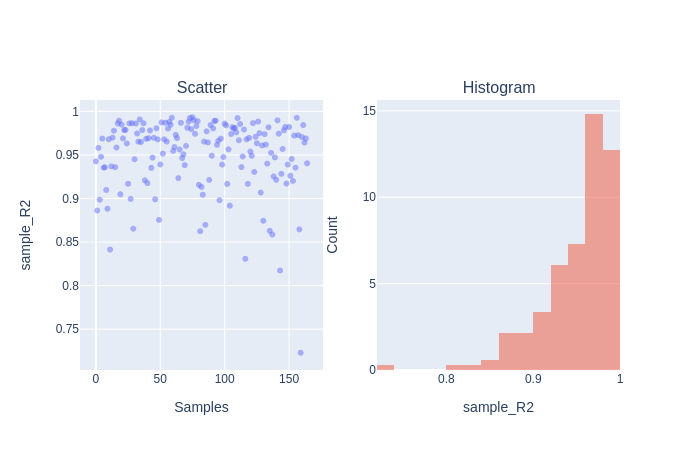
The all-point-mixed R² coefficient on the pressure of the surface car was 0.916.

The distribution of the R² score over the samples is given in the figure also, with a visual comparison.

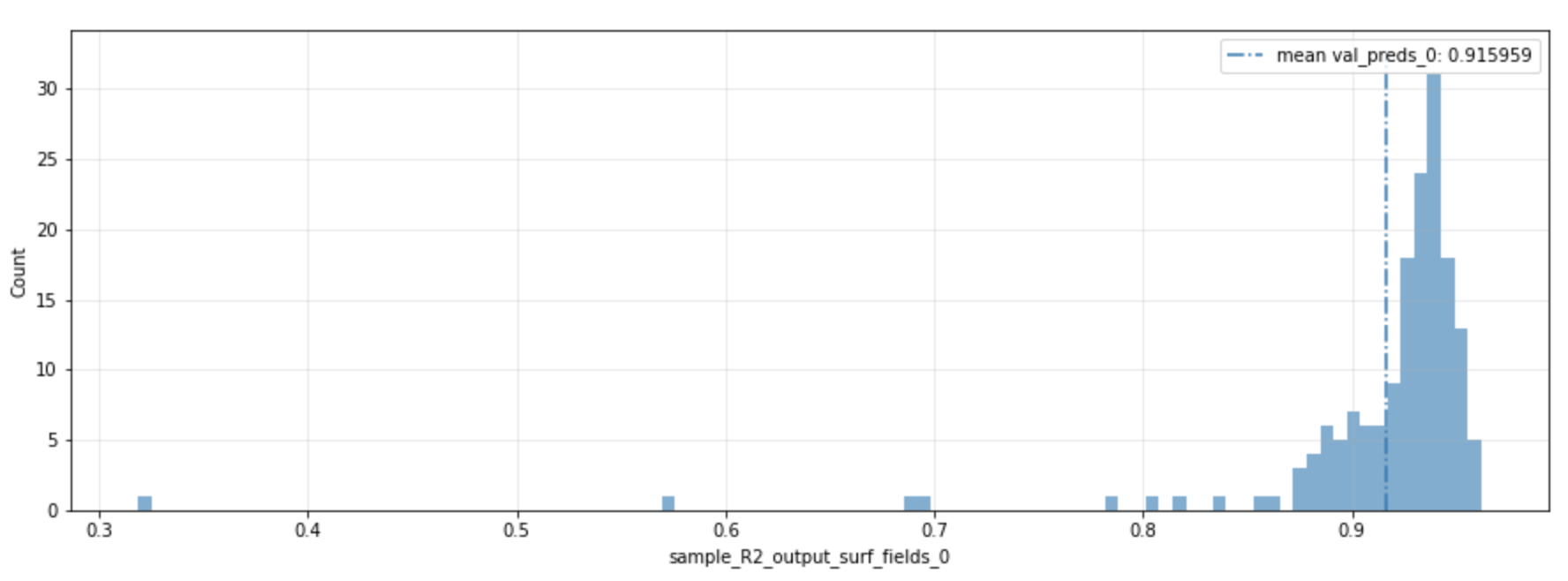
What is R²? R-squared, R2-score or R² is a statistical measure representing the proportion of the variance in the dependent variable that is predictable from the independent variable(s) in a regression model. R² ranges from 0 to 1, where “0” means the model does not explain any of the variances, and “1” means the model explains all the variance. In deep learning, R² is used to evaluate the model’s goodness of fit to the training data. The closer R² is to 1, the better the model fits the data.

We predicted the pressure on the vertical plane just behind the tyre as a second step.

The all-points-mixed R² coefficient on the plane was 0.9674995. The R² distribution over the samples is given in the Appendix, with visual comparisons between CFD and neural network predictions.

F1 Use Case: Implementation

NCS is accessible under various forms, including:

• standalone Web App
• local App customized for aerodynamicists
• additional filter in ParaView

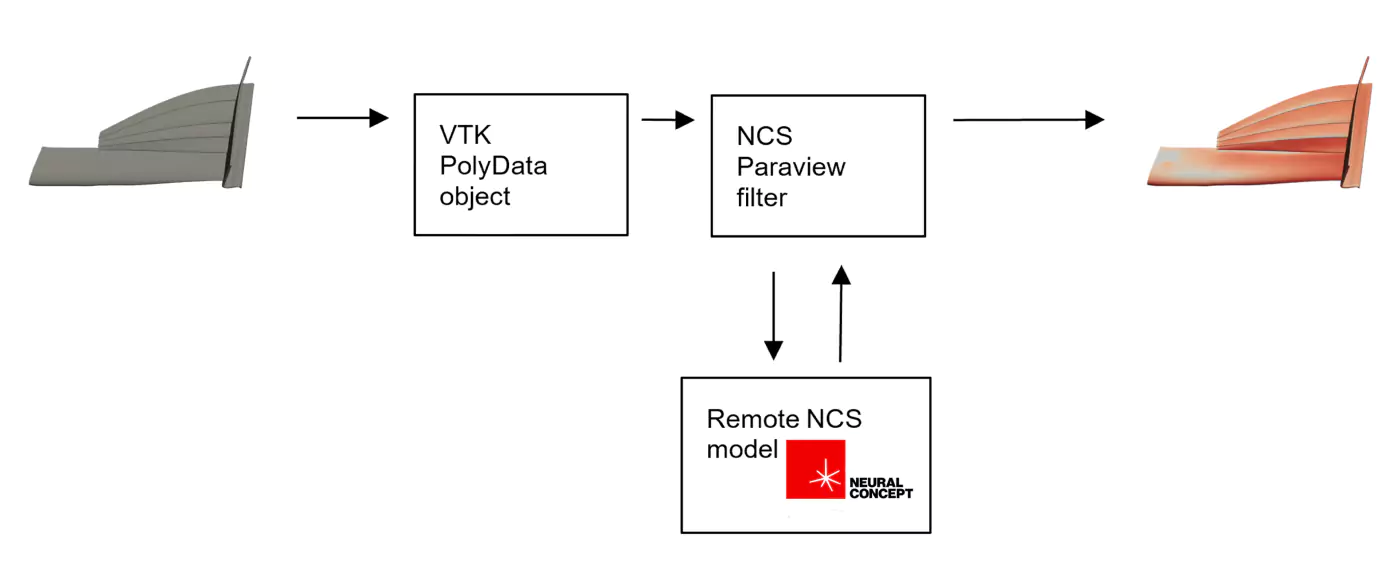
Therefore, deep learning integrated into ParaView provides the “look and feel” of a postprocessor but allows the import of nonparametric shapes such as STL and IGES and post-process them immediately.

F1 Use Case: Conclusion

We analyzed the capabilities of geodesic CNNs to predict almost in real-time (0.1 s) the aerodynamics of an F1 car, compared with hours needed to run a CFD simulation on an HPC cluster. NCS predictions compared very well with available CFD data.

An end-to-end workflow demonstrated the capability of NCS to predict flow fields by using as only input the car's geometry.

Although the simulations considered here are a simplified version of the higher fidelity more detailed models used by competitive teams, it opens the door to the perspective of re-using all the legacy simulations produced and stored by Formula 1 teams over the years.

With Deep Learning simulations such as NCS, it will be possible to explore more geometries and converge faster towards promising designs without re-running an excessive number of simulations.

Appendix: Use Case Illustrations

‍

‍