Conjugate Heat Transfer: Basics, Best Practices & Applications

Heat transfer is the phenomenon of energy exchange due to temperature differences. Heat transfer is seldom restricted to a single material or medium. Real-world systems involve continuous interactions between solids and fluids. Conjugate heat transfer (CHT) captures this dynamic. CHT models how heat flows between solid structures and the surrounding fluids as a cohesive system. In this article, we will break down the fundamentals of heat energy across multiple media. We will explore applications of this mode of energy transfer. Also, we will discuss how applying machine learning in CFD can enhance CHT analysis for engineering.

What is Conjugate Heat Transfer?

Conjugate Heat Transfer, or CHT, is the concurrent heat energy exchange between a solid and adjacent fluid(s). It integrates conductive heat transfer in the solid and convective heat transfer in the fluid. A key aspect of CHT analysis is heat flux continuity at the interface, representing thermal interactions between media.

For instance, CHT can be encountered in various types of heat exchangers.

What is Heat Exchange and why It Occurs (Macroscopic Explanation)

Energy exchange occurs due to the second law of thermodynamics. This law dictates that heat flows from higher to lower temperatures, increasing entropy. This transfer happens via conduction, convection, or radiation. The outcome is that systems move toward thermal equilibrium.

Let us start with a crude representation of two “cells” or blocks. Cell 1 has a temperature T₁, and cell 2 has a temperature T₂ (no temperature profiles develop inside the cells or blocks). This initial situation has a lower entropy S.

There is a difference ΔT = T₁ - T₂, and the natural tendency is for ΔT → 0, leading to thermal equilibrium. As energy flows as heat, entropy increases to a new value S’ > S, reaching a maximum at equilibrium.

What are the CHT Outputs

Coupling conduction and convection, CHT is a tool for predicting temperature spatial distribution, heat transfer rates, and critical thermal parameters. These parameters are essential for optimizing designs in the automotive, aerospace, civil engineering, electronics cooling, and energy industries. 

Don't Avoid Radiation

In many cases, radiation heat transfer is also essential. This is particularly true when radiation can become the dominant transfer mode at high temperatures! So, while CHT focuses on conduction and forced and natural convection, advanced simulations can incorporate thermal radiation. Radiation must be considered in industrial furnaces, spacecraft thermal design, and high-temperature reactors to avoid significant errors in heat transfer predictions.

Naive Example

A convection oven in our kitchen is a simple example of fully combined heat transfer. Forced convection (via a fan) and natural convection (via buoyancy) circulate air; conduction transfers heat through metal surfaces and food, while radiation from the oven walls and heating elements directly heats the meal.

This illustrates how radiation interacts with conduction and convection. Fluids are generally transparent to radiation, while solids are opaque, leading to surface-to-surface radiation in cavities. However, both can be semitransparent, allowing radiation to be absorbed, emitted, and scattered.

Even if negligible at low temperatures, radiation dominates when temperature differences are significant. Conduction and convection are proportional to ΔT, i.e., they exhibit linear proportionality to the temperature difference, while radiation follows a nonlinear relationship, scaling as T⁴.

How Does Conjugate Heat Transfer Work?

Conjugate heat transfer refers to the combined interactions between fluids and solids. Conduction, forced and natural convection, and occasionally radiation coexist. While fluids depend on forced and natural convection to transfer heat, solids conduct heat. Many situations need a unified approach to thermal analyses. Below, we investigate the fundamental modes of heat transfer. Later, we will show typical heat exchanger design software from CFD to Deep Learning.

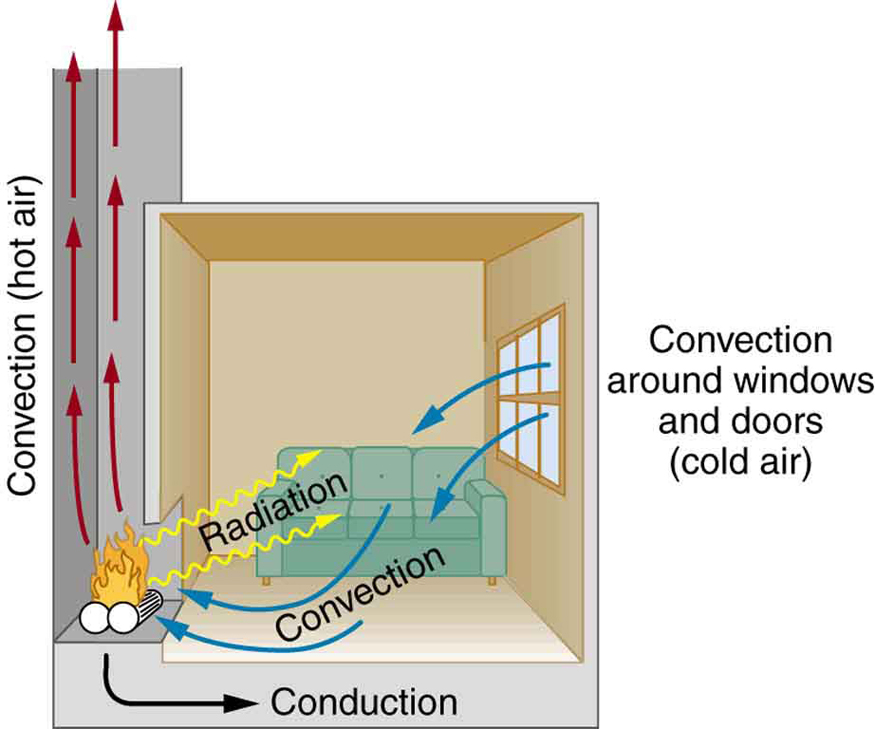
Heat Transfer Process in Fluids

Heat transfer occurs through conduction and convection in fluids, with convective heat transfer often dominating due to bulk fluid motion. The fluid usually plays the role of an energy carrier over large distances. Buoyancy forces drive natural convection, while forced convection is typically fluid flow induced by external forces, such as fans for air flow and pumps for liquid coolant flow. Convection allows fluids to distribute heat more than conduction alone. Forced convection is the most common way to achieve a high heat transfer rate in thermal management applications.

Depending on the flow conditions, water can exhibit convective heat transfer coefficients between 100 and 10,000 W/(m²·K) in forced convection.

Pure conduction in liquids like water is significantly lower, typically ranging from 0.5 to 5 W/(m²·K).

The following equation (Newton’s law of cooling) quantifies convective heat transfer:

Q = h A ΔT

Q = heat transfer rate, h = convective heat transfer coefficient, A = heat transfer surface area, and ΔT = the difference in temperature between the fluid and surface. The temperature difference (ΔT) between the fluid and the surface is a driving force behind convection.

Ultimately, the convective heat transfer rate depends on ΔT, A, and the complex interactions governing the convective heat transfer coefficient h—fluid velocity, turbulence intensity, and surface conditions—determining how effectively heat moves within a fluid system.

The convective heat transfer coefficient h encapsulates multiple physical effects, including fluid motion, boundary layer behavior, and turbulence. As fluid flows over a surface, it forms a boundary layer—a thin region where velocity and temperature gradients develop. The nature of this layer (laminar or turbulent) significantly influences heat transfer. With intense mixing and enhanced interaction, turbulent flow increases h, leading to larger heat exchange.

Heat Transfer Process in Solids

Heat conduction in solids transfers thermal energy from hot to cool areas. Wood, brick, wool, and steel contain different insulation levels. Fourier's Law describes heat flux in solids based on the temperature gradient (∇T). Heat flux is proportional to the temperature gradient and the material's thermal conductivity.

This law aids engineers and scientists in designing thermal systems. Heat conduction explains thermal energy transmission in metals and insulators.

Research by pioneers like Joseph Fourier advanced our understanding of heat transfer. Jean-Baptiste Biot's 19th-century experiments measured heat flow through materials, laying the groundwork for thermal conductivity. Fourier's Law links heat flux, temperature gradient, and thermal conductivity.

Thermal Conductivity

Thermal conductivity is a material property that quantifies a substance’s ability to conduct heat. It is measured in Watts per meter-kelvin (W/(m·K)).

The thermal conductivity value of solids can vary depending on the material. Metals like copper and aluminum exhibit high values while insulating materials like wood and foam have much lower values.

While thermal conductivity is often associated with solids, this is a misconception. Thermal conductivity may be underestimated in gases and liquids because convective heat transfer dominates. In these cases, effective heat transfer capability involves thermal conductivity and the influence of fluid motion, which enhances heat distribution. Thus, while fluids may have lower thermal conductivity values than solids, their ability to transfer heat through convection can be considerable.

Fundamental Differences: Conductive and Convective heat transfer

The linearity in conduction and convection stems from their governing equations (Fourier’s law and Newton’s law of cooling), which describe how heat transfer responds linearly to temperature differences. However, the underlying physics is different!

Conduction relies on energy transfer through molecular interactions in materials. The linear relationship occurs because the heat transfer rate is proportional to differences in temperature, fundamentally linked to the material properties, i.e., thermal conductivity k. Thermal conductivity is a measurable material property that tells us how much a substance can conduct heat at a given temperature.

Convection concerns the bulk movements of fluid and energy transfer resulting from this fluid motion. The linear relationship in convection assumes the heat transfer rate increases directly with the temperature difference between the surface and the fluid. Warmer fluid rises while cooler fluid sinks, creating convective currents. The convective heat transfer coefficient (h) is a measurable property that characterizes the effectiveness of convective heat transfer in a fluid. It incorporates factors related to fluid motion, flow dynamics, and fluid properties, making it way more complex than the thermal conductivity of solids!

For the eager, simulation-conscious readers, let us anticipate that modeling conduction numerically can be effectively handled without CFD while simulating convection requires it, becoming significantly more complex and challenging, especially in natural convection.

Interaction Between Solids and Fluids

When solids and fluids interact thermally, heat transfer occurs at their interface, combining conduction within the solid and convection in the fluid. This interplay appears in heat exchangers, cooling systems, and thermal insulation applications. The solid conducts heat internally at the interface, while the fluid transports heat away through convective motion.

Modeling CHT requires solving coupled heat transfer equations for both domains. This ensures accurate predictions of temperature distribution and thermal performance in complex systems.

The efficiency of this process depends on:

• Thermal conductivity (k) of the solid – High-conductivity materials (e.g., metals) facilitates rapid heat distribution, while insulators (e.g., ceramics) slow it down.

• Convective heat transfer coefficient (h) of the fluid – Higher values indicate enhanced heat exchange, influenced by fluid velocity, turbulence, and properties.

• Contact surface area (A) and temperature difference (ΔT): Heat transfer is driven by larger interfaces and greater temperature differences.

Steady-State and Transient, Heat Sinks and Heat Sources

A typical CHT scenario involves a heated solid surface in contact with a cooling fluid. Heat spreads within the solid via conduction, reaching the interface where it is transferred to the fluid. Flow characteristics such as turbulence and boundary layer development in forced convection significantly impact heat dissipation.

A typical CHT scenario concerns cooling. A heated surface is in contact with a cooling fluid to cool a solid. Heat spreads within the solid via conduction, reaching the interface and transferring it to the fluid. Flow characteristics such as turbulence and boundary layer development in forced convection significantly impact heat dissipation.

The phenomenon can be transient, where the system starts in a non-equilibrium state and evolves toward equilibrium, or steady, where continuous heat input and removal create a stable temperature distribution. For example, if a heat source exists on the solid side, CHT helps determine how to optimally conduct heat to the heat sink, which is often aided by devices like fans or pumps. Solid heat sinks are usually made of metal with high thermal conductivity, such as copper or aluminum.

Example of Conjugate Heat Transfer in Action

A clear example of conjugate heat transfer at work is the thermal response difference in a house with stone walls during summer. Sun-heated walls absorb heat, but the air's higher thermal diffusivity leads to slower temperature changes indoors. This "buffering effect" helps keep the interior cooler. The stone gradually releases stored heat at night, stabilizing indoor temperatures and preventing fluctuations. The stone's greater thermal inertia ensures stable interior temperatures despite changes outside.

Governing Equations for Conjugate Heat Transfer

When analyzing conjugate heat transfer, the objective is to simultaneously solve the heat conduction equation in solids and the conjugate convective heat transfer equation in fluids.

The governing equation for heat conduction is the Fourier unsteady-state equation:

∇ (k∇T) = ρc ∂T/∂t

where material properties are k = the thermal conductivity of the solid material, ρ = the material density, and c = the specific heat capacity, we want to solve for temperature T=T(x,y,z;t), i.e., a temperature distribution over space with a spatial gradient∇T and over time with a time derivative ∂T/∂t.

The boundary conditions for solid and fluid domains must be appropriately defined to ensure a consistent and accurate analysis.

Numerical Methods for 3D Heat Transfer Simulations

Solving conjugate heat transfer problems in three dimensions requires numerical methods for  handling coupled conduction and convection equations. Analytical solutions are often impractical for complex geometries. Computational approaches like the Finite Volume Method (FVM), Finite Element Method (FEM), and Finite Difference Method (FDM) are standard.

1. FVM is most used in CFD. It discretizes governing equations over control volumes, ensuring energy conservation across each cell. Thus, the Finite Volume Method suits fluid flow and convection-dominated issues. 

2. FEM divides the domain into elements and applies weighted residual techniques to approximate temperature fields, offering flexibility for complex geometries and anisotropic materials.

3. The Finite Difference Method (FDM) uses Taylor series approximations to replace differential equations with algebraic equations on a structured grid. While simple, it is less adaptable to irregular geometries than FVM and FEM, which is why FVM and FEM are more used in commercial codes for engineers.

Simulation Setup and Best Practices for CHT

Accurate simulations in conjugate heat transfer require a systematic approach that follows precise guidelines. By following these practices, engineers can effectively utilize this analytical method and gain insightful information about heat transfer interactions in solid and fluid domains.

Geometry Preparation

A well-prepared geometry is crucial for accurate CHT simulations. Ensure all solid-fluid interfaces are adequately defined and remove unnecessary geometric details that could increase computational cost without improving accuracy. Avoid sharp edges or thin walls that could cause meshing issues and numerical instabilities.

Mesh Quality

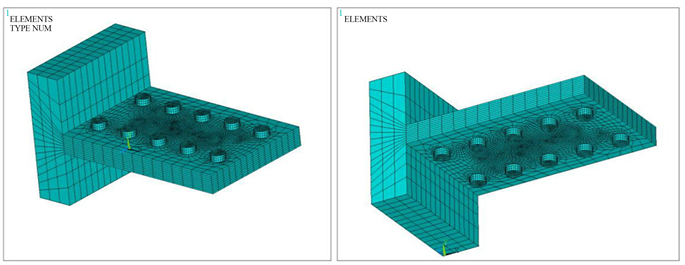
Mesh generation forms the basis of any simulation. In conjugate heat transfer, a well-structured mesh is crucial for capturing the geometry and resolving temperature and velocity gradients. A balanced mesh is necessary — sufficiently detailed to represent complex features without high computational costs.

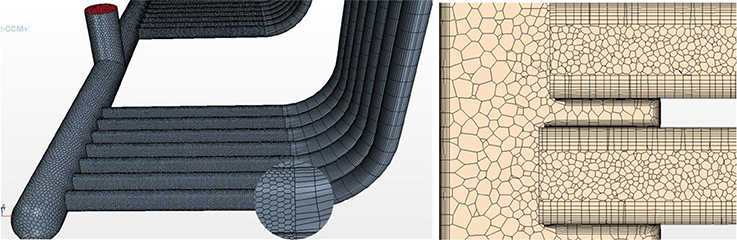
CAE has advanced in conjugate heat transfer simulation. The model analyzes a vehicle's chassis to determine how heat affects solid and plastic components. High-quality meshes are crucial for intricate geometries. Thin-layer meshing creates high-resolution elements in thin solids, allowing engineers to capture thermal gradients, heat transfer, and fluid dynamics while maintaining computational efficiency.

Mesh Refinement and Element Sizing Guidelines

Increase mesh density at solid-fluid interfaces to accurately resolve temperature jumps and heat flux.

Best practice iN MESHING: Boundary Layer Resolution

Use inflation layers for accurate velocity and temperature gradients near walls in convection-dominated cases (see above figure).

Best practice iN MESHING: Thin Solids Meshing

Structured hexahedral or prism elements are used in thin regions to maintain accuracy without excessive element count.

Best practice iN MESHING: Gradual Transitions

Avoid abrupt changes in element size to prevent numerical instabilities and ensure smooth solution convergence.

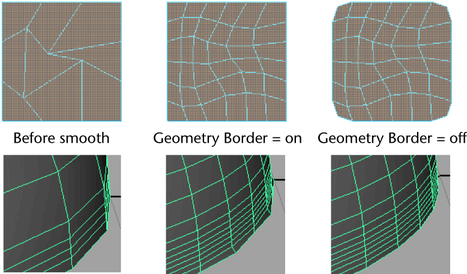
Best practice iN MESHING: Adaptive Refinement

Utilize solver-based adaptive meshing to refine areas with high thermal gradients dynamically.

Boundary Conditions

Defining boundary conditions, like wall temperature, is vital for reliable simulation. Accurate conditions reflect the physical situation, ensuring the integrity of the temperature field. Solid and fluid domains require careful treatment of the interface in conjugate heat transfer. Conditions in solids specify temperatures or heat fluxes at surfaces interacting with fluid.

CFD tools can treat flow and solid domains as interconnected, exchanging wall temperatures at interfaces governed by different physical laws. Convective conditions address heat exchange with fluid, incorporating the convective heat transfer coefficient and ambient temperature. In fluid domains, conditions include inflow/outflow velocities, wall temperature, and pressure.

Solver Settings

Choosing the right solver and convergence criteria can guarantee accurate conjugate heat transfer simulations. The choice between segregated and coupled solvers hinges on the intensity of the solid-fluid interaction. Coupled solvers ensure stability in strong interactions, while segregated solvers lower costs in weaker coupling. Regarding flow regimes, pressure-based solvers suit low-speed flows, while density-based solvers effectively manage high-speed compressible flows.

If radiation is significant, especially at high temperatures, include DO (Discrete Ordinates) or S2S (Surface-to-Surface) models.

Turbulence Modeling

Turbulence modeling cannot be ignored in heat transfer because it influences fluid behavior and mixing. This leads to differences in heat transfer coefficients ranging from 2 to 10 times higher than those in laminar flow conditions. Heat transfer is primarily governed by conduction in laminar flow, with lower Nusselt numbers (Nu), typically around 3.66 for fully developed laminar flow in a circular pipe. In contrast, turbulent flow can achieve Nu> 100. This means stronger convective heat transfer due to increased mixing and energy transport.

The k-ω SST turbulence model ensures reliable boundary layer resolution, effectively capturing flow characteristics near walls and providing accurate predictions in turbulent regimes.

Hybrid RANS/LES models can be very effective at capturing transient effects, such as unsteady flow patterns and vortex dynamics, leading to improved predictions of heat transfer rates and overall system behavior in complex thermal environments.

Reaching Convergence

Convergence criteria require precise definition.  Momentum, energy, and turbulence residuals should be below 10⁻⁴ to 10⁻⁶, with energy ideally at 10⁻⁶ for reliable predictions.

Verifying heat flux balance at solid-fluid interfaces confirms thermal equilibrium. Monitoring temperature and velocity profiles ensures consistency, while adjusting iterative under-relaxation factors can enhance stability in complex cases. Proper tuning leads to realistic CHT simulations.

Transient Heat Transfer

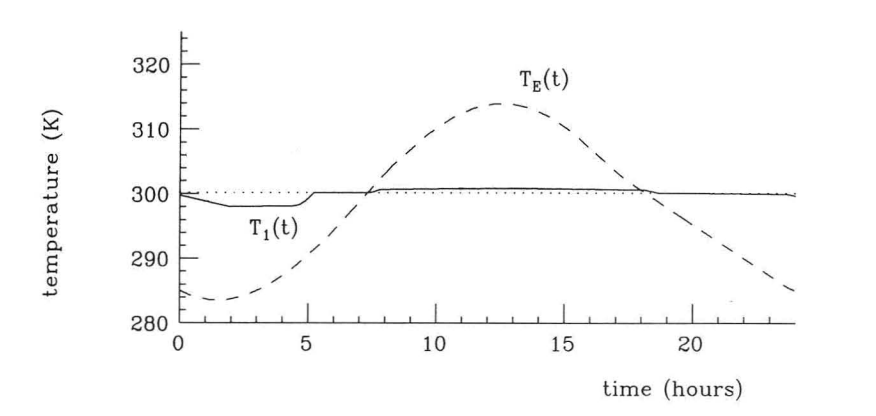
Transient phenomena in solids and fluids exhibit varying time scales. Solids typically exhibit slower thermal responses due to higher thermal diffusivities, whereas fluids respond more rapidly. In the summertime, a house with massive stone walls remains cool due to the stone's high thermal inertia. During the day, the solid walls absorb heat from the sun, but due to the slow thermal response of the solid, the interior remains cooler than the outside air.

The walls gradually release stored heat at night, maintaining a comfortable interior temperature. In fluid heat transfer, transient conduction describes the temporal evolution of temperature through a fluid medium due to temperature differences.

Transient Conduction Equations

The transient conduction equation is a partial differential equation representing this phenomenon is the known ∇( k∇T)= ρ c (∂T/∂t) where ρ, c, and k are the usual material properties (density, specific capacity, and conductivity) for the fluid. Adding a heat sink or heat source term "q," it becomes:

∇ (k∇T) + q = ρ c (∂T/∂t)

The unsteady-state heat conduction equation for the solid is, in a similar fashion, with the possibility of a heat sink or heat source term "q":

∇ ( kₛ ∇T) + q = ρₛ cₛ (∂T/∂t)

Now, transient phenomena in heat transfer manifest distinct time scales in solids and fluids, with their thermal responses governed by thermal diffusivity and material properties. This phenomenon is illustrated in the cooling behavior of a house with massive stone walls during summertime, shedding light on the interplay between heat transfer mechanisms.

Due to their comparatively higher thermal diffusivities, solids exhibit slower thermal responses.

Solid-Flow Interface

The temperature field and heat flux maintain continuity at the solid-flow interface. Nevertheless, within a moving fluid, the temperature field can exhibit rapid fluctuations: in proximity to the solid, the fluid's temperature closely mirrors that of the solid, whereas farther from this interface, the fluid's temperature aligns with the inflowing or ambient fluid temperature.

The thermal boundary layer is the spatial range over which fluid temperature transitions from solid-equivalent to bulk-fluid temperature. The thermal boundary layer dimensions, which are about the dimensions of the momentum boundary layer, are expressed with the Prandtl number.

The Prandtl number reflects the ratio of momentum diffusivity to thermal diffusivity. Achieving a Prandtl number of 1 necessitates equivalence between thermal and momentum boundary layer widths. A thicker momentum layer would yield a Prandtl number surpassing 1. Conversely, a Prandtl number below 1 signifies a thinner momentum boundary layer than the thermal boundary layer.

As a reference, the Prandtl number for air at atmospheric pressure and 20°C is 0.7.

For water at 20°C, the Prandtl number is about 7.

These values reflect the relative importance of momentum diffusivity (kinematic viscosity) to thermal diffusivity in each fluid.

Mathematics of Conjugate Heat Transfer: Looking for Analytical Solutions

The heat diffusion equation describes how temperature evolves within a medium. Solving it analytically can be complex, but solutions exist for simple cases with well-defined boundary conditions. Let’s consider a rod of length L, initially at a uniform temperature T₀, with one end fixed at a constant temperature (Dirichlet condition) and the other insulated (Neumann condition). We use variable separation to determine the temperature distribution over time, breaking the solution into spatial and time-dependent parts.

The resulting solution expresses temperature as a sum of modes, each decaying over time due to heat conduction. These modes describe heat energy phenomena along the rod, with faster-decaying modes smoothing out temperature variations more quickly

The key takeaways are:

• Heat spreads over time, with sharp temperature differences fading away.

• The solution consists of multiple “modes,” each contributing to the overall temperature profile.

• Higher modes decay faster, meaning the rod gradually approaches thermal equilibrium.

This approach helps predict how heat evolves in practical applications such as thermal insulation, metal cooling, and heat exchangers.

Numerical Methods: Solving Complex Equations

Conjugate heat transfer simulations use numerical approaches for heat conduction and convection. Finite Element Analysis (FEA), also known as "structural analysis," addresses heat transfer in solids, while Computational Fluid Dynamics (CFD) models fluid and air energy transport, including phase changes. Accurately representing temperature fields in solids yields more precise fluid thermal boundary layer temperatures.

Choosing appropriate numerical techniques and solvers ensures accuracy. Thoughtful selections of discretization schemes and algorithms clarify energy transport in conjugate systems.

More Insight Into FEA and CFD and Temperature Distribution Prediction

FEA and Computational Fluid Dynamics (CFD) are powerful numerical techniques for modeling complex thermal phenomena. These methodologies are widely used in engineering and scientific disciplines to analyze intricate systems' temperature distribution, fluid flow, and heat exchange.

FEA involves partitioning a given domain into discrete elements, enabling precise approximations of temperature profiles. This procedure, known as discretization, allows the representation of intricate geometries and material properties. The complete temperature profile of each element can be expressed using interpolation functions, with the system's behavior characterized by a set of algebraic equations.

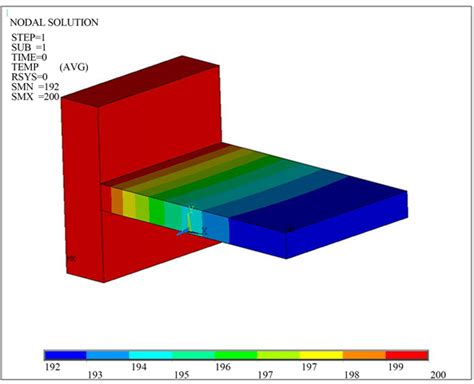
CFD uses mesh divisions to model turbulent flows and energy transport. The Navier-Stokes and energy equations with appropriate additional models to "close" the turbulence physics by approximations govern turbulent fluid flow, accounting for heat exchange and complex interactions between motion and thermal effects.

Incorporating the energy equation provides a comprehensive representation of fluid behavior and energy transport thus:

rate of change + convective transport = conductive transport + sources i.e.:

ρc ∂T/∂t + u⋅∇T = ∇⋅(k ∇T) + q

AI and CAE Simulation

Deep learning, a subset of AI, mimics human cognition to detect patterns, predict outcomes, and generate insights. It outperforms traditional methods in precision. Combined with CAE simulation, it allows engineers to explore new designs.

Inspired by human visual processing, 3D Deep Learning with Convolutional Neural Networks (CNNs) identifies image patterns and effectively manages complex CAD geometries, helping engineers enhance simulations.

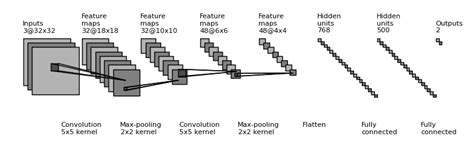
Neural Concept combines CNNs and computer vision to analyze CAD models in real time. This enables engineers to quickly identify design flaws and optimization opportunities that traditional CFD and CHT methods might miss due to computational constraints.

Engineering Applications of Conjugate Heat Transfer

Conjugate heat transfer has widespread applications in various engineering fields, including electronics cooling, thermal management of engines, and aerospace design.

Conjugate heat transfer, coupled with modern simulation tools, is an indispensable analytical tool in engineering domains rooted in technical precision, from electronics cooling to aerospace engineering and industrial processes. For instance, conjugate heat transfer allows engineers to optimize cooling solutions and extend the lifespan of electronic components.

The sections below provide more information, and the Neural Concept website is dedicated to other data-driven workflow applications.

Cooling Systems Applications

CHT analysis is critical for thermal management in power electronics and IC packages, particularly for hotspot mitigation in high-power-density applications like GaN transistors and multi-core processors. Engineers use these simulations to optimize thermal interface materials (TIMs) and evaluate junction-to-ambient thermal resistance in various cooling solutions. Engineers use conjugate heat transfer simulations to analyze geometries, such as heat sinks and microchannels, coupled with fluid flow dynamics.

Heat Exchangers Applications and Conjugate Heat Transfer

The field of heat exchangers, integral to diverse industrial processes, benefits from conjugate heat transfer analysis. The effective thermal energy exchange between fluid streams is essential in applications from HVAC system design to chemical processing.

With CHT simulation, engineers evaluate heat transfer coefficients, pressure drops, and thermal gradients, enabling precise parameter tuning for optimal performance.

This comprehensive analysis culminates in better energy usage and reduced operational expenditures.

Typical examples of heat exchangers and their simulations are:

1. Shell and Tube Heat Exchangers are used in oil refining and chemical processing. CHT analysis optimizes flow arrangements and tube layouts, enhancing heat transfer while minimizing pressure losses. 

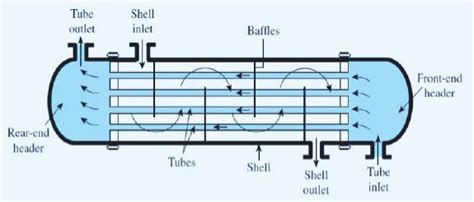
2. Plate Heat Exchangers are standard in food and beverage processing. They benefit from CHT simulations that optimize plate design and spacing. The analysis identifies optimal flow paths for maximizing heat transfer and minimizing fouling, which is crucial for product quality and reduced cleaning costs.

3. Air-cooled heat Exchangers: These are used in power plants and HVAC systems. They utilize ambient air for heat dissipation. CHT analysis optimizes fin design and airflow patterns, enhancing cooling performance while considering environmental factors like wind and temperature fields.

4. Double Pipe Heat Exchangers often heat or cool one fluid through another. CHT simulations enable precise modeling of heat transfer and fluid dynamics. Analyzing fluid interaction allows engineers to optimize the design for maximum thermal performance, reducing energy consumption.

Automotive Applications: Braking System Conjugate Heat Transfer Simulation

The first of two applications concerning car design and car manufacturing is brakes.

During aggressive braking events, the friction couple (rotor-pad interface) experiences thermal loading that can exceed 600°C, leading to thermal fade and potential pad glazing. CHT analysis helps optimize brake caliper designs and rotor ventilation geometry to maintain optimal brake torque coefficient while preventing thermal shock-induced disc coning.

1. Ventilation and Cooling: Evaluation of the effectiveness of cooling mechanisms, such as ventilation channels or ducts, to mitigate temperature rise in critical brake components.
2. Materials: Suitable materials with optimal thermal properties for enhanced heat dissipation and durability.
3. Performance Enhancement: Improved braking performance, reduced wear, and extended component lifespan.

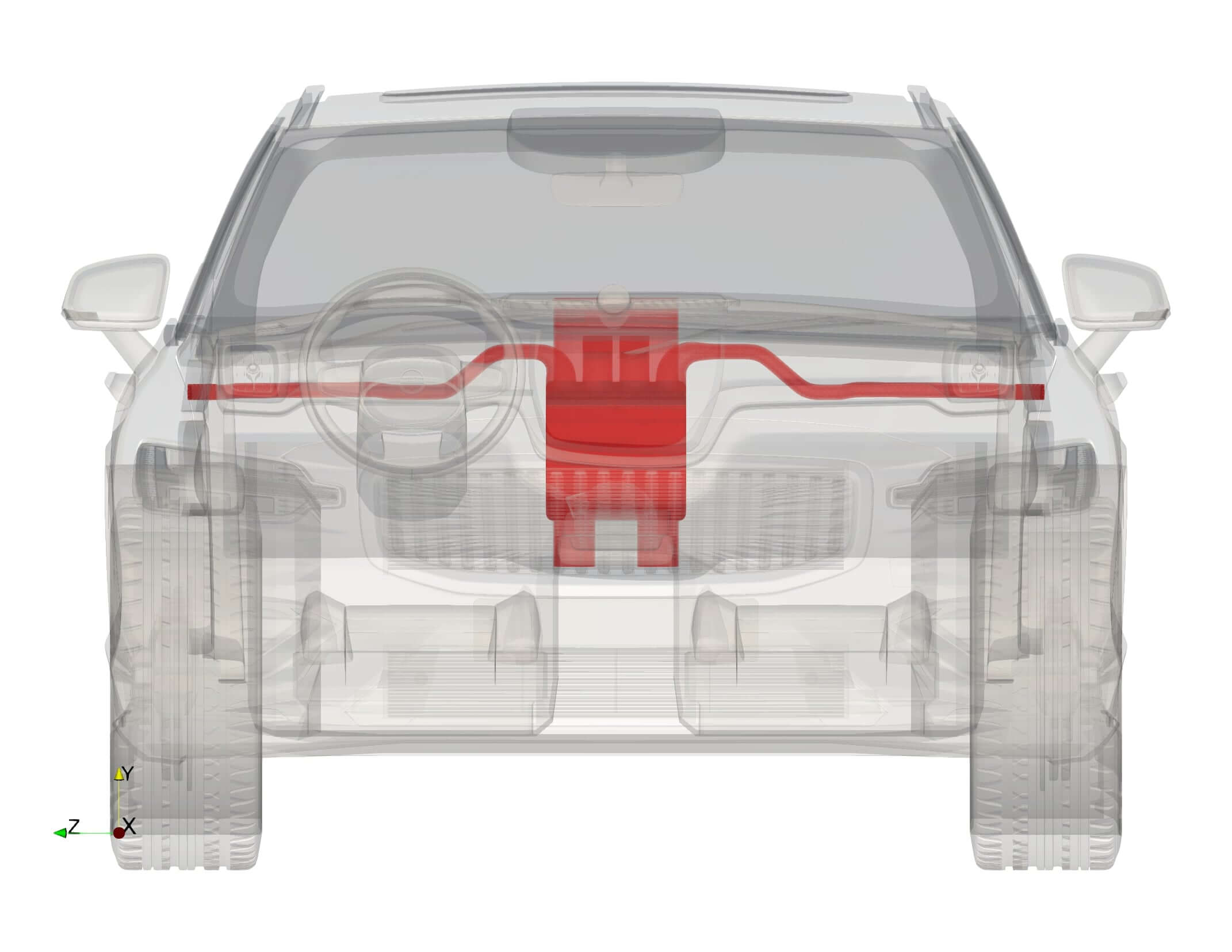
Underhood Conjugate Heat Transfer Simulation

CHT simulations provide vital insights for developing vehicle thermal management.

Internal combustion engines generate heat, which is reflected in the vehicle's underhood area, which houses heat sources like the engine and exhaust system. Engineers utilize conjugate heat transfer (CHT) simulation to optimize cooling performance and ensure adequate heat dissipation from critical components.

CHT simulation models heat transfer in the engine bay, evaluating how heat is conducted through components and convected by air or coolant.

Analysis can identify potential overheating issues and assess the cooling system's effectiveness by simulating engine load and airflow patterns.

Moreover, CHT simulations help design components like radiators and fans for maximum heat exchange.

Industrial Process Conjugate Heat Transfer Problems

Conjugate heat transfer analysis is crucial for industrial processes, impacting manufacturing and energy conversion. This analysis models solid components and fluid flows in equipment, providing insights into heat transfer rates, temperature distributions, and thermal stresses. Engineers use these insights to optimize designs and operational parameters and lower energy consumption.

Examples of Conjugate Heat Transfer in Industrial Processes

Engineers employ conjugate heat transfer analysis in metallurgy to enhance cooling strategies in processes like continuous casting. This method simulates the heat exchange between metal and cooling water. Likewise, engineers utilize this method in the chemical processing sector to manage reaction kinetics and temperature variations, leading to improved yield, selectivity, and safety.

Conjugate heat transfer analysis (CHT) is fundamental in thermal modeling in power generation. In gas turbines, first-stage nozzle guide vanes and rotor blades are exposed to gas path temperatures exceeding the material's creep limit. CHT analysis optimizes internal cooling channel geometries, including serpentine passages and pin-fin arrays, to maintain acceptable metal temperatures while minimizing parasitic pressure losses. Engineers use these simulations to evaluate film cooling effectiveness η and overall cooling effectiveness φ.

This approach minimizes thermal stresses and boosts the turbine's performance and lifespan.

Conclusions on CHT

In this article, we have progressed from physics to mathematics to numerical solutions and, finally, the CHT engineering applications.

CHT analysis is the ultimate solution for engineers optimizing designs with "rock-solid" reliability for thermal simulations. This multidisciplinary approach combines CFD simulations with thermal analysis of solids. It enables engineers to understand the interaction between fluid flows and solid components, improving brake systems' performance and underhood thermal management in automotive engineering.

CHT analysis will remain crucial in fields like industrial processes and aerospace exploration, and we believe that adopting AI is the best path to engage all engineers aiming for optimal results.

FAQ

What are the three types of heat transfer?

Conduction is mainly heat transfer through solids. Convection is heat transfer via fluid movement, free or forced. Radiation is energy transfer through electromagnetic waves.

Why is CHT important in engineering simulations?

CHT models interactions between solid and fluid domains, ensuring accurate thermal predictions for heat exchangers, turbines, and electronics cooling.e

How can I ensure convergence in my CHT simulation?

Refine mesh near solid-fluid interfaces. Use appropriate turbulence models. Apply accurate boundary conditions and monitor residuals and energy balance.

What software tools are used for CHT analysis?

ANSYS Fluent, COMSOL Multiphysics, OpenFOAM, and Simcenter STAR-CCM+ simulate CHT in engineering applications. They can all feed the Neural Concept platform for data-driven predictions.

Which is better, a higher heat transfer coefficient or a lower one?

Higher coefficients enhance heat dissipation, while lower values improve thermal insulation. The optimal value depends on the application.

‍