Deep Neural Network in Simulations
Deep learning and AI in general have taken the entire field of computer science by storm and has now become the dominant approach to solving a wide array of problems, ranging from winning board games to molecular discovery. However, Computer Assisted Design (CAD) and geometry processing are still mostly based on traditional techniques.
Indeed, numerical simulation techniques have traditionally relied on solving physically derived equations using finite differences and adding heuristic models when those become too complex to solve (Turbulence models in fluid mechanics for example). More recently, Lattice Boltzmann methods have become popular as a means to simulate streaming and collision processes across a limited number of particles. Both classes of techniques remain (computationally) (very) expensive (we are talking about hours to days of simulation), and since the simulation must be re-run each time an engineer wishes to change the shape, this makes the design process slow and costly.
A typical engineering approach is therefore to test only a few designs without a fine-grained search in the space of potential variations. Hence the company is limited by:
- Its financial resources for the given project
- The time constraints of the project
- Its engineers’ experience and cognitive biases during the product development phase.
Since this is a severe limitation, there have been many attempts at overcoming it and one of the most famous is reduced-order modeling:
Reduced-Order modeling (ROM) is a class of Machine Learning approaches used to learn a simplified model of a simulator, based on data. This method is a simplification of a high-fidelity dynamical model, built from a large number of numerical simulations. It preserves essential behavior and dominant effects, for the purpose of reducing solution time or storage capacity required for the more complex model. It is applied in a large range of physics and has proven its efficiency for specific applications. It works well when the engineer wants to vary a few, well-defined parameters, with a specific objective in mind. A good overview of the different techniques used is given in this paper: https://www.sciencedirect.com/science/article/abs/pii/S0376042103001131
However, the modeling power of classical ROM methods is limited, and they present several drawbacks:
- For some industries, the majority of the simulation data is acquired through experiments, by sensors being placed at various locations, conditions... This data cannot be easily transferred to a reduced-order model. Indeed, it would require that the conditions of experiments are always strictly identical, which is very rarely the case, as you need a total control over the parameters and conditions of simulation
- When building the reduced-order model, a parameterization is defined and kept throughout the whole project and the simulations have to be generated using this parametrization. If a company is facing new requirements for a given product, or wants to explore new designs, they may be forced to change their parameterization. Then, they would have to start everything from scratch again and re-generate a bunch of simulations to build a new ROM. It creates silos in the company’s workflow, where ROMs are built for very specific use-cases and are hardly used for later applications.
- Some applications require the simulations of very complex phenomena, with discontinuities that may appear (transonic flows...). ROMs tend to « smooth » these discontinuities, giving large errors in these specific regions.
Deep Neural-Networks are an extension of classical Reduced Order Modeling, where the approximating function is not limited to a simple linear model but can be extended through a stack of non-linear operations, called layers. A very recent branch of the Deep-Learning research applies this concept to the processing of geometric information and was able to overcome the limitations of more classical reduced-order models. Based on a neural network architecture, it is able to understand 3D shapes and learns how they interact with the laws of physics. Since it uses raw, 3D, unprocessed geometries as input, it does not suffer from all of the previous drawbacks I mentioned. The engineer is now able to leverage on its historical database (even if the parametrization of a given part has evolved over time!) and integrate experimental data as well. 3D Deep Learning allows to switch from silos workflows to a common base where the information is globally shared and continuously re-used.
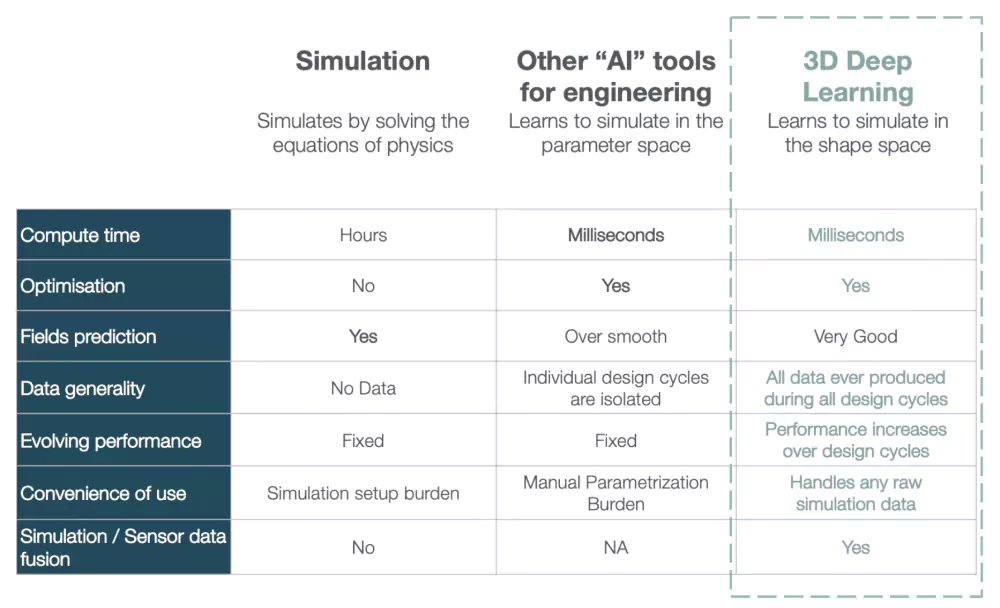
It is also orthogonal to the physics, and the same technique can tackle a very large range of physics. Finally, its overall performance is able to improve over time, as it can be fed with new simulations on the fly.
Conclusion
After these few lines, it seems like 3D Deep Learning is the solution to enhance engineering processes! Well it is, but there is also a very important step in order to exploit the full potential of this tool (but also of any machine learning technique): preparing your data so that the model can extract the maximum of information out of it. In a follow-up article, I will come with a few tips and tricks to get the best out of your data when using Machine Learning for numerical simulations.
Stay tuned!

.png)

